WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Re: Integraal van 1/(1-x²) bepalen

Dit is een reactie op vraag 60084

U verwijst o.a. naar galileo.math.siu.edu. Dit geeft voor mij de beste uitleg. Alleen ... ; ik blijf steken in de Appendix on Rotations! Omdat er geen tekening is bijgevoegd, kan ik niet goed begrijpen wat er bedoeld wordt met:
a = x cos draaiingshoek - y sin draaiingshoek en
b = x sin draaiingshoek + y cos draaiingshoek.
Wie kan mij dit met een tekening duidelijk maken? Bij voorbaat heel veel dank!
Johan
Student hbo - zondag 13 september 2009

Antwoord

Beste Johan,

Ik heb het onderstaande figuur aangepast uit hetzelfde document waar ik de vorige keer naar heb verwezen (galileo.math.siu.edu).
Je kunt je als volgt voorstellen wat er gebeurd is: je stopt een punaise in de oorsprong en draait met het assenstelsel tegen de klok in. Dan heb je over een bepaalde hoek, zeg $\theta$ gedraaid. De coördinaten van $A$ en $B$ zijn hierdoor veranderd, die nieuwe punten geef ik aan met $A'$ en $B'$.

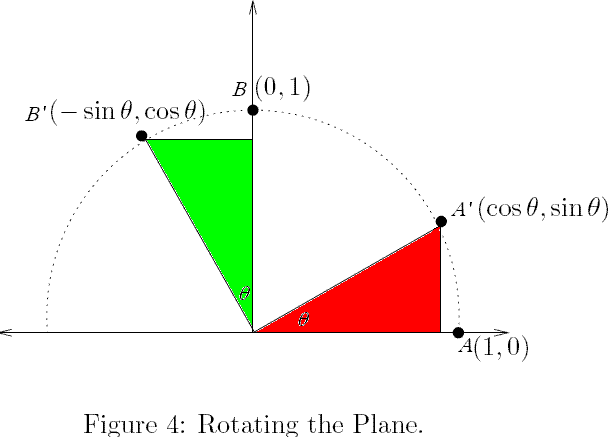
Als je naar de rode driehoek kijkt, dan zie je dat hij rechthoekig is. En vanuit punt $A'$ kan men op de $x$-as en $y$-as projecteren.
In die rode driehoek geldt dus dat $\cos(\theta) = \frac{\mbox{aanliggende rechthoekszijde}}{\mbox{schuine zijde}}$ dus $\cos(\theta) = \frac{\mbox{aanliggende rechthoekszijde}}{1}$. En de aanliggende rechthoekszijde is de $x$-coördinaat van $A'$. Dus $x_{A'} = \cos(\theta)$
De overstaande rechthoekszijde t.o.v. $\theta$ is de $y$-coördinaat van $A'$.
Dus $\sin(\theta) = \frac{\mbox{overstaande rechthoekszijde}}{\mbox{schuine zijde}}$ m.a.w. $\sin(\theta) = \frac{\mbox{overstaande rechthoekszijde}}{\mbox{1}}$. Dus de overstaande rechthoekszijde heeft als lengte $\sin{\theta}$. Dus $y_{A'} = \sin(\theta)$.

Datzelfde truukje haal je bij de groene driehoek uit, waarbij je je wel moet realiseren dat als je de overstaande rechthoekszijde t.o.v. $\theta$ op de x-as projecteert dat je in het negatieve gedeelte van de $x$-as ligt.

In de vectorvoorstelling hebben we dus het volgende $\color{red}{{1 \choose 0} \to {\cos(\theta) \choose \sin(\theta)}}$ en $\color{green}{{0 \choose 1} \to {-\sin(\theta) \choose \cos(\theta)}}$.
En aangezien ${x \choose y} = x \cdot \color{red}{{1 \choose 0}} + y \cdot \color{green}{{0 \choose 1}}$,
moet gelden dat ${x \choose y} = x \cdot \color{red}{{\cos(\theta) \choose \sin(\theta) }} + y \cdot \color{green}{{-\sin(\theta) \choose \cos(\theta)}}$.
Oftewel ${x \choose y} = {x \cdot \cos(\theta) - y \cdot \sin(\theta) \choose x \cdot \sin(\theta) + y \cdot \cos(\theta)}$.

Mocht je vragen hebben, reageer gerust!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 13 september 2009