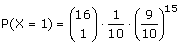WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Kans op rood

Dit is een reactie op vraag 59675

Stel je zit met 3 groepen ballen A,B,C (stel elke groep bestaat uit 500 000 ballen) waaruit meerdere mensen ballen nemen, je weet echter niet hoeveel rode ballen erin zitten (stel 50 000 rode ballen). Je hebt hierbij 2 verschillende situaties, namelijk de volgende:

1) de eerste persoon kiest ervoor om in 1 keer 16 ballen te trekken.
2) de tweede persoon kiest ervoor om in groep A en B telkens 5 ballen te nemen, en uit groep C 6.

Wie maakt dan het meeste kans om 1 rode bal te nemen?
John
Iets anders - zondag 21 juni 2009

Antwoord

Bij zulke grote aantallen kan je de kansen wel benaderen alsof het met terugleggen is. De kans op een rode bal in elke groep is dan ¹/₁₀ en de kans op niet rood is dan ⁹/₁₀.

1.
Als je alle 16 ballen uit groep A haalt dan kun je de kans op precies 1 rode bal berekenen met de binomiale verdeling:

X:aantal rood
p=¹/₁₀
n=16
Gevraagd: P(X=1)

2.
Bij de tweede manier moet je dat dan ook doen, maar weer op dezelfde manier als bij je vorige vraag.

P(1 rode bal uit A)=P(1 van de 5 uit A is rood)·P(5 geel uit B)·P(6 geel uit C)
Dat doe je dan voor P(1 rood uit B) en P(1 rood uit C) ook. Optellen en je bent al weer een eind op weg.

Je zult zien dat het weinig uitmaakt. Ik kom voor beide uit op ongeveer 0,329.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 21 juni 2009