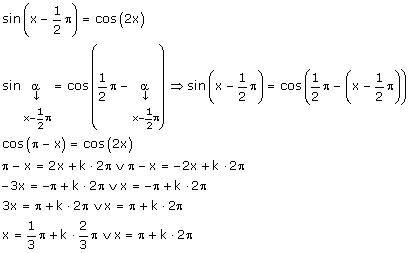WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Een goniometrische vergelijking oplossen

Dit is een reactie op vraag 59484

-cosx = -cos(-x)??

ik dacht de regel cos(-t) = cos t te gebruiken, maar ik vind dat eigenlijk veel moeilijker dan sint = cos(1/2p-t) die isveel gemakkelijker om te gebruiken om om te schrijven!

als ik 't verder uitwerk kom ik uit op
of x = -p+2kp

maar het antwoordenboek zegt iets anders???

mijn uitwerkngen zijn
cos(p-x) = cos2x
p-x = 2x + 2kp
-3x = -p +2kp
x = -1/3p -2/3kp

p-x = -2x + 2kp
p+x = 2kp
x = -p +2kp

Céline
Leerling bovenbouw havo-vwo - maandag 1 juni 2009

Antwoord

Dit soort vergelijkingen hebben 'oneindig' veel oplossingen. Om dat een beetje handig op te schrijven gebruik je k·2p met kÎ. Maar 'waar' je begint met 'opnoemen' is niet van belang.

De oplossing -p+k·2p is dezelfde oplossing als p+k·2p. Je bent dan alleen 2p 'verder' begonnen met 'opnoemen'. Hetzelfde geldt voor die -¹/₃p modulo ²/₃p, je kunt ook 'beginnen' bij ¹/₃p.

In plaats van -k·2p kan je ook rustig k·2p schrijven. Toch?

Ik zal je mijn uitwerking geven...

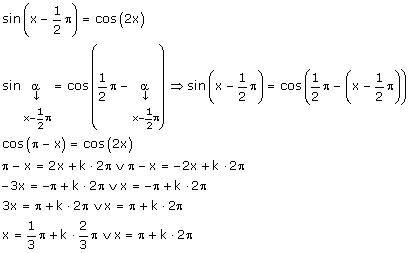
Ook een ander antwoord maar ook goed. Je moet daar bij goniometrische vergelijkingen dus nog een beetje mee uitkijken.

Naschrift: het antwoord is een beetje dubbelop! Zie reactie hieronder.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 1 juni 2009

Re: Re: Een goniometrische vergelijking oplossen