WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Een goniometrische vergelijking oplossen

Los op

sin(x-p/2) = cos (2x)
geleerd: schrijf zo dat er staat sint = sin u of cost = cosu

ik kies voor cost = cosu
sin(x-p/2) = -sin(1/2p-x) = -cosx,
vraag 1: vervolgens zou ik dit laten staan, je hebt inmiddels een cos. maar het antwoordenboek schrijft vervolgens -cos om naar cos(p+x) waarom? en als het vanwege de -1 voor de cosinus is, waarom schrijf je -cosx dan niet om naar cos(-x)?

2. als ik dan verder ga rekenen krijg je
-cosx = cos(2x)
t = u + 2kp of t = -u+2kp
x = 2x + 2kp of x = -2x + 2kp
-x = 2kp 3x = 2kp
x = -2kp x = 2/3kp

als antwoord staat er: x = p+ 2kp of x = -1/3p + 2/3kp

dat is iets anders dan wat ik heb gevonden, waar gaat het nou mis?
Céline
Leerling bovenbouw havo-vwo - maandag 1 juni 2009

Antwoord

Wat er mis gaat is dat -cosx=cos(2x) nog niet de vorm cos(...)=cos(...) heeft. Je moet 'echt' naar die vorm toe.

Ik zou 't zo doen:

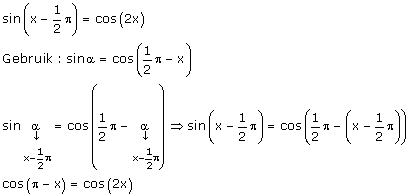
...en dan verder uitwerken. Hopelijk is dat duidelijk?

Maar er zijn natuurlijk vele wegen die naar Rome leiden.

Pas op!
-cos(x) is toch niet hetzelfde als cos(-x)?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 1 juni 2009

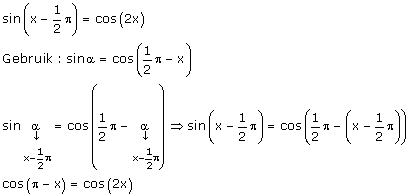
Re: Een goniometrische vergelijking oplossen