WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Re: Baansnelheid

Dit is een reactie op vraag 58952

Ik snap de uitleg, maar niet hoe je kunt zien dat de helling in het punt x=0, niet gelijk is aan 0.

En betekent dit dus dat als er in een opdracht gevraagd wordt naar een maximum of minimum, dat je niet altijd de afgeleide gelijk moet stellen aan 0? Maar het antwoord soms moet vinden door naar de eigenschappen van de grafiek moet kijken? Ik vind het moeilijk om te beslissen in welke gevallen ik welke keuze moet maken.

Bedankt!!!
Céline
Leerling bovenbouw havo-vwo - maandag 13 april 2009

Antwoord

Waar het eigenlijk om gaat is dit:
Een extreme waarde kan optreden als de afgeleide in een punt ter weerszijden van dat punt een verschillend teken heeft: dan gaat de grafiek over van stijgend in dalend of omgekeerd.
Dat kan het geval zijn als de afgeleide in een punt 0 is of (en dat is bij die absolute waarde het geval) de afgeleide in een punt niet bestaat.

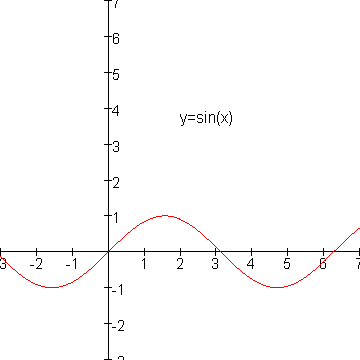
Je kijkt naar de eigenschappen van de grafiek als die op eenvoudige wijze te herleiden is tot een standaardgrafiek zoals bijvoorbeeld sin. Dat was in dit geval inderdaad zo:
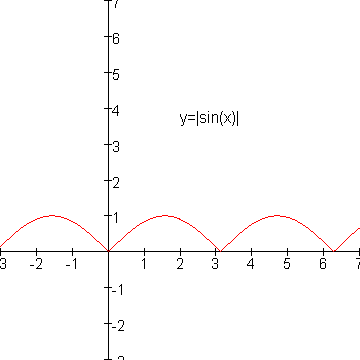
De grafiek van |sin(x)| ontstaat uit de grafiek van sin(x) door de stukken onder de x-as "naar boven om te klappen".
Vergelijk onderstaande plaatjes maar eens.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 13 april 2009