WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Baansnelheid

Dit is een reactie op vraag 58940

Heel erg bedankt.

Ik kom nu uit op t = 1/2p of t = 1/1/2p
de parametervoorstelling was

x = 3sint - sin3t
y = 3cost - cos3t

dus coordinaten:
x = 3sin(1/2p) - sin(3·1/2p) = 4
y = 3cos(1/2p) - cos(3·1.2p) = 0
geeft (4,0)

x = 3sin(1/1/2p) - sin(3·1/1/2p) = -4
y = 3cos(1/1/2p) - cos(3·1/1/2p) = 0
geeft (-4,0)

Dan nog een laatste vraag over de aanpak. Ik ben nu een beetje in de war met het zoeken van minima en maxima. Zou je deze ook opgelost kunnen hebben met het zoeken van de afgeleide en deze dan gelijk stellen aan 0?

Bedankt!!

Céline
Leerling bovenbouw havo-vwo - maandag 13 april 2009

Antwoord

De vraag over de maxima wel.
Hoewel het in dit geval simpeler is om uit te gaan van de eigenschappen van de sinusgrafiek.
Als de vraag was geweest in welke punten is de snelheid minimaal, dan was dat niet gelukt.
Kijk maar eens in de grafiek.
De minimale waarde van v is nul. In die punten waar v=0 is de helling beslist geen 0.
In feite is in die punten de helling van de grafiek van v niet gedefinieerd.

Iets dergelijks kom je ook tegen bij de grafiek van f(x)=|x|

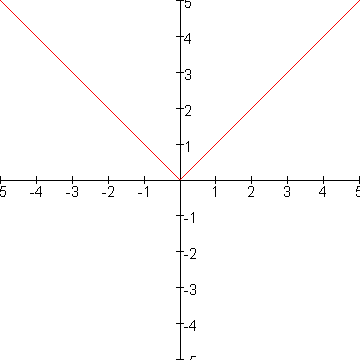
Je ziet hier dat het minimum van f gelijk is aan 0 voor x=0.
Toch is de helling in dat punt geen 0. In feite is de helling daar niet gedefinieerd.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 13 april 2009

Re: Re: Re: Baansnelheid