WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Afgeknotte hexaëder met zijden van twee

Ik moet de oppervlakte en de inhoud uitrekenen van een regelmatig afgenotte kubus. De uitslag bestaat uit:

6 gelijkzijdige achthoeken met zijde 2
8 gelijkzijdige driehoeken met zijde 2

Hoe moet ik dit uitrekenen? Ik hoop dat iemand me kan helpen.
den yi
Leerling bovenbouw havo-vwo - dinsdag 7 april 2009

Antwoord

Eerst maar 's een tekening:

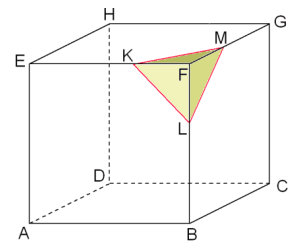
De totale oppervlakte van de afgeknotte kubus is de som van de oppervlakten van die 6 achthoeken en de 8 driehoeken.

De oppervlakte van één zo'n regelmatige achthoek:

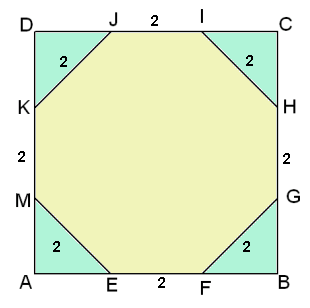
Kijk 's in driehoek FBG. FG=2 en FB=BG, dus FB=Ö2 en BG=Ö2. Waarom? De oppervlakte van ABCD is dan (2Ö2+2)²=8Ö2+12. Waarom? Driehoek FBG heeft een oppervlakte van 2. Waarom? Dus de oppervlakte van zo'n achthoek is gelijk aan 8Ö2+4. Waarom?

De oppervlakte van één zo'n gelijkzijdige driehoek met zijde 2 kan je vinden op Oppervlakte van een gelijkzijdige driehoek. Dat is in dit geval dan Ö3. Waarom?

Dan kan je oppervlakte wel uitrekenen.

De inhoud:
De zijde van de kubus was 2Ö2+2. Dus de inhoud van de kubus is... Daarvan af halen de inhoud van de 8 piramides. Kijk eens naar de piramide F.KLM. Je kunt dit ook opvatten als de piramide met grondvlak KFM en hoogte FL. De oppervlakte van het grondvlak KFM hebben we hierboven al berekend en de hoogte van FL is ook bekend... dus kan je de inhoud van één zo'n piramide wel bepalen denk ik.

Volgens mij moet je dan een heel eind kunnen komen! Hopelijk lukt het zo!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 7 april 2009