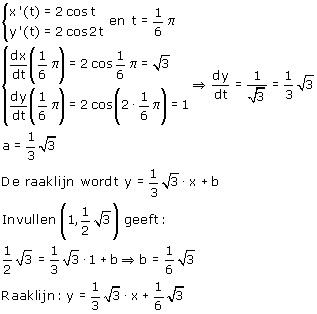|
|
|
\require{AMSmath}



Raaklijn aan een kromme
Hallo,
De opdracht is: Als de grafiek niet door de oorsprong gaat, geef je het functievoorschrift van de richtingscoŽfficiŽnten bereken je de punten waarvoor geldt: 0.5 rc het is een parameterkromme, maar hoe pak je dat dan aan bij zo'n functievoorschrift?
x(t)=4sin(0.5t)
y(t)=3cost
Want kijk, als je een gewone functie had, gebruik je toch f'(a)∑(x-a)+f(a) , maar hoe doe je dit nou? En als je rc 0.5 wil hebben neem ik aan dat je voor de y 0.5 invult... Of ben ik helemaal in de war geraakt?
Alvast bedankt
Zeyno
Leerling bovenbouw havo-vwo - zondag 1 februari 2009
Antwoord
De vergelijking van een willekeurige raaklijn aan de kromme is gelijk aan y=ax+b. Hierin in a de richtingscoŽfficiŽnt en (0,b) het snijpunt met de y-as.
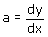
Voor een willekeurig punt van de kromme is de richtingscoŽfficiŽnt van de raaklijn gelijk aan:
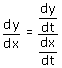
De waarden van 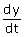 en en 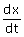 in het punt kan je bepalen. Met het invullen van het raakpunt kan je dan ook b bepalen. in het punt kan je bepalen. Met het invullen van het raakpunt kan je dan ook b bepalen.
Voorbeeld
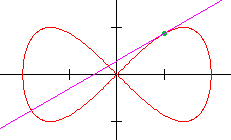
Geef de vergelijking van de raaklijn aan de kromme in het punt $(1,\frac{1}{2}\sqrt{3})$.
Uitwerking
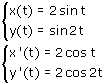
Maar wat is nu de waarde van t?
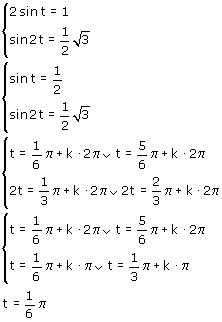
Nu kan je 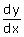 berekenen: berekenen:
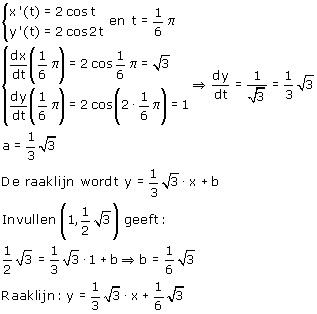

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 1 februari 2009
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








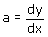
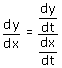
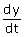 en
en 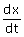 in het punt kan je bepalen. Met het invullen van het raakpunt kan je dan ook b bepalen.
in het punt kan je bepalen. Met het invullen van het raakpunt kan je dan ook b bepalen.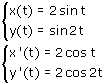
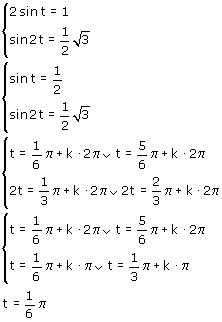
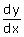 berekenen:
berekenen: