WisFaq!

Raaklijn aan een kromme

Hallo,
De opdracht is: Als de grafiek niet door de oorsprong gaat, geef je het functievoorschrift van de richtingscoëfficiënten bereken je de punten waarvoor geldt: 0.5 rc het is een parameterkromme, maar hoe pak je dat dan aan bij zo'n functievoorschrift?

x(t)=4sin(0.5t)
y(t)=3cost

Want kijk, als je een gewone functie had, gebruik je toch f'(a)·(x-a)+f(a) , maar hoe doe je dit nou? En als je rc 0.5 wil hebben neem ik aan dat je voor de y 0.5 invult... Of ben ik helemaal in de war geraakt?

Alvast bedankt

Zeyno
1-2-2009

Antwoord

De vergelijking van een willekeurige raaklijn aan de kromme is gelijk aan y=ax+b. Hierin in a de richtingscoëfficiënt en (0,b) het snijpunt met de y-as.



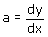
Voor een willekeurig punt van de kromme is de richtingscoëfficiënt van de raaklijn gelijk aan:



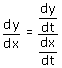
De waarden va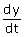n en 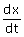in het punt kan je bepalen. Met het invullen van het raakpunt kan je dan ook b bepalen.

Voorbeeld

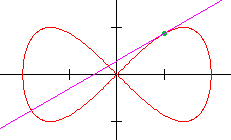
Geef de vergelijking van de raaklijn aan de kromme in het punt $(1,\frac{1}{2}\sqrt{3})$.

Uitwerking



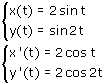
Maar wat is nu de waarde van t?



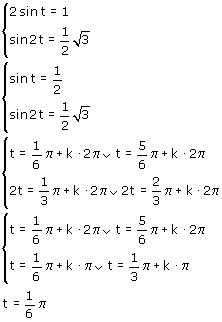
Nu kan je 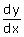berekenen: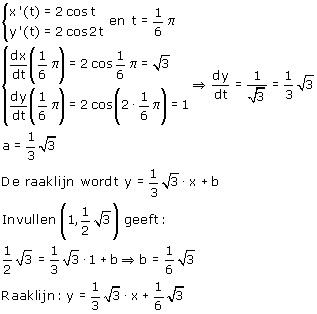

WvR
1-2-2009