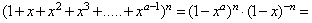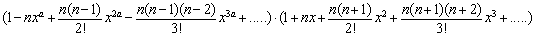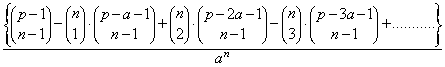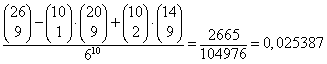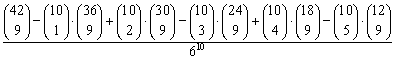|
|
|
\require{AMSmath}



Werpen met 4 dobbelstenen
Ik werp met 4 dobbelstenen tegelijk. Op hoeveel verschillende manieren liggen er samen 30 ogen op tafel ?
Door alle mogelijke gevallen uit te schrijven kom ik op 8.
Maar deze methode is onbruikbaar wanneer de getallen groter worden, bijvoorbeeld werp met 10 dobbelstenen 40 ogen.
G.Th.J
Ouder - zondag 25 januari 2009
Antwoord
Men doet een worp met n dobbelstenen, ieder met a zijvlakken waarop de getallen 1,2,3,….a zijn aangebracht. Hoe groot is de kans dat door de dobbelstenen tezamen p geworpen wordt?
Er zijn an gevallen, daar bij elke steen ieder der a zijvlakken kan boven komen.
Het aantal gunstige gevallen is gelijk aan de coëfficiënt van 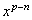 in de ontwikkeling van in de ontwikkeling van
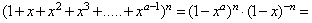
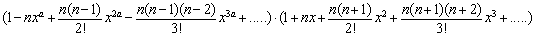
De kans is dan gelijk aan
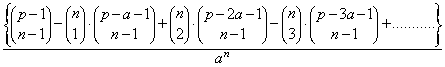
waarbij de sommering moet worden voortgezet zolang de getallen tussen de haakjes niet negatief zijn.
Als handigheidje om handmatig rekenwerk in te tomen dient nog de opmerking dat de kans niet verandert als men p vervangt door n(a+1) – p.
Bij gewone dobbelstenen komt het dan neer op het omdraaien van alle stenen, zodat een worp p overgaat in een worp 7n-p. Dit omdat tegenoverstaande vlakken een optelsom 7 hebben.
Bij wijze van voorbeeld het volgende geval: gooi 10 dobbelstenen waarmee je in totaal 43 wilt werpen.
We nemen dus n = 10, a = 6 en p = 43.
Door 43 te vervangen door 70 – 43 = 27 krijgen we voor de kans:
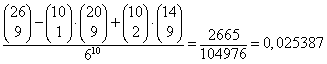
Was 43 niet eerst verkleind tot 27, dan was de berekening veel taaier geweest, namelijk:
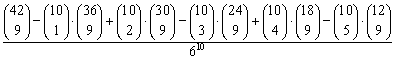
Zie ook Kans op een bepaald aantal ogen.
MBL
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 28 januari 2009
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|








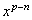 in de ontwikkeling van
in de ontwikkeling van