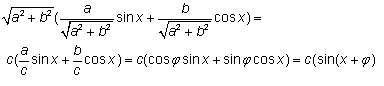WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Berekenen van een functie die langs alle toppen van een gegeven functie gaa

Dit is een reactie op vraag 57278

Ik heb zonet een groepsbijeenkomst gehad en heb mij aanpak die ik dus van u heb gekregen uitgelegd. Ze vonden de uitwerking wel goed alleen kenden de volgende formule niet:
p·sin(x)+q·cos(x)=c·sin(x+$\Phi$), waarin c=√(p²+q³) en $\Phi$=arctan(p/q)

Ik kan deze formule ook niet in ons Calculus boek (Adams, A Complete Course, Sixth Edition) vinden. Weet u misschien een betrouwbare bron waar deze formule te vinden is of van af te leiden is? Zodat ik een goede onderbouwing heb voor de functie die door de toppen gaat voor in mijn verslag.

Djarek
Djarek
Student universiteit - donderdag 27 november 2008

Antwoord

Beste Djarek,
Je kent denk ik wel de somformule sin(p+q)=sin(p)cos(q)+cos(p)sin(q)

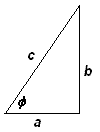
In het plaatje zie je dat a/c=cos$\Phi$ en b/c=sin$\Phi$, met c=SQRT(a²+b²).
Nu geldt:

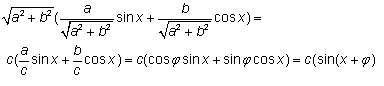
Ik heb het uit een oud goniometrie schoolboek van drs.P.E. Lepoeter.
Succes.Lieke

De gedempte exponentiele functie gaat trouwens niet precies door de toppen, maar raakt aan de sinus grafiek.

ldr

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 27 november 2008

Re: Re: Berekenen van een functie die langs alle toppen van een gegeven functie