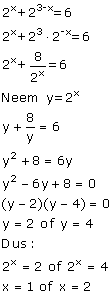WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Exponentiele vergelijking

Dit is een reactie op vraag 56515

Ik zie wel wat je doet. Maar een paar dingen zijn nog niet helemaal duidelijk waarom. De vergelijking heb ik geprobeerd op te lossen aan de hand van een voorbeeld wat ze erbij gaven:

2^x+2^3-x=6
2^x+8·2^-x=6

Stel 2^x=a, dan:
a+8·a^-x=6
a²-6a+8=0
(a-2)(a-4)=0
2^x=2 Ú a=4
x=1 Ú x=2

Bij bovenstaand voorbeeld stellen ze 2^-x gelijk aan a^-1 en vermenigvuldigen ze deze vervolgens weg door alles met a te vermenigvuldigen.

Waarom bij het voorbeeld wel en bij mijn opgave niet? Hoe kan ik dit het gemakkelijkst onderscheiden? Ook zie ik dat je verder niks meer doet met de 2160?
Broes
Student universiteit - donderdag 18 september 2008

Antwoord

Hoho! Als je de vergelijking y·27=2160+y/3 oplost dan doe je toch echt wel iets met die 2160!

y·27=2160+y/3
81y=6480+y
80y=6480
y=81

Dus ik bedoel maar...

Bij het voorbeeld doe je hetzelfde. Alleen nu staat er ook een 'min' in de exponent. Dat maakt het dan iets ingewikkelder, maar niet fundamenteel anders.

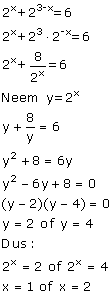
Maar er zijn (zoals altijd) meer wegen die naar Rome leiden.
Helpt dat?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 18 september 2008