WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Papierbalen

Dit is een reactie op vraag 52416

Hoezo is 2/(1,5h²) hetzelfde als 4/(3h²)? En wat bedoelen ze met 10 cm overlap?

Verder zou ik niet uit deze oplossing kunnen komen!

Help me , please!! Ik zou jullie erg dankbaar zijn!!
Maar niet alleen voor het antwoord, maar ook HOE jullie tot het antwoord zijn gekomen!!

Dan weet ik dat voor een volgende keer!
Hugo F
Student hbo - woensdag 10 oktober 2007

Antwoord

Hugo,

2/(1,5h²)=4/(3h²). Ik heb gewoon boven en onder de deelstreep met 2 vermenigvuldigd om dat kommagetal (1,5) kwijt te raken.
De ijzeren banden zijn steeds 0,1 meter (10 cm) langer dan de omtrek van de baal.

Even een plaatje zoals ik me de situatie voorstel:

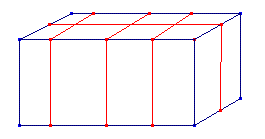
De rode lijnen zijn de ijzeren banden.
Ik heb er drie op de derde manier om de baal gelegd en een op manier twee (zie vorig antwoord).
Ik weet niet wat de bedoeling is!
Nu is de totale lengte van de ijzeren banden:
3×2(b+h)+2(l+h)+0,4=6{4/(3h²)+h}+2(1,5h+h)+0,4=
=8/h²+6h+5h+0,4=8/h²+11h+0,4
Hiervan zoeken we het minimum.
Differentieren geeft:
-16/h³+11=0
Dus 16/h³=11
h=³Ö(16/11)1,13 meter.
Dan is de lengte 1,70 meter en de breedte 1,04 meter.

Zo duidelijk?
Als de banden anders om de balen moeten kan je het nu denk ik zelf berekenen!

ldr

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 10 oktober 2007