|
|
|
\require{AMSmath}
Bewijs oppervlakte vierhoek ABCD mbv sinus
Gegeven:
Opp. driehoek ABC=1/2·a·c·sin(B) waarbij AB=c en BC=a .
Ik wil graag het bewijs dat de oppervlakte van een vierhoek ABCD gelijk is aan het halve produkt der diagonalen maal de sinus van de hoek door de diagonalen gevormd.
En hoe kan ik uit dat bewijs een meetkundige methode afleiden om een vierhoek in een driehoek te veranderen.
Herman
Leerling bovenbouw havo-vwo - zondag 30 september 2007
Antwoord
Beste Herman,
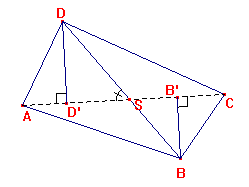
Zie plaatje. Hoek S=$\angle$ASD=$\angle$BSC. S is snijpunt diagonalen.
Oppervalk $\Delta$ACD=1/2×AC×DD'=1/2×AC×DS×sin(S)
Oppervalk $\Delta$ABC=1/2×AC×BB'=1/2×AC×SB×sin(S)
Gevolg: oppervlak ABCD=1/2×AC×(DS+SB)×sin(s)=1/2×AC×BD×sin(s).
Als je nu in de applet (Cabri figuur) punt B naar C schuift, dan zie je dat BD samen valt met CD en AC valt smaen met AB.
De vergelijking gaat dan over in: oppervalk $\Delta$ACD=1/2×AC×CD×sin($\angle$ACD).
Is dat wat je bedoelde?
ldr
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 30 september 2007
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Re: Bewijs oppervlakte vierhoek ABCD mbv sinus