 |
De digitale vraagbaak voor het wiskundeonderwijshome | vandaag | gisteren | bijzonder | gastenboek | wie is wie? | verhalen | contact |
||||||||||||||||||
|
\require{AMSmath}



Kleurenpoker met 4 maal 7 kleurenkaartenKleurenpoker is een spel met 4 maal 7 kleurenkaarten. Als er 7 willekeurige kaarten getrokken worden wat is dan de kans op een carre met een triple, de kans op 7 verschillende kleuren, de kans op een carre en een paar, de kans op een triple met twee paar, de kans op 2 triples, de kans op een carre, de kans op 3 paar, de kans op een triple en een paar, de kans op een triple, de kans op 6 verschillende kleuren, op 5 verschillende kleuren, de kans op 2 paar en tenslotte te kans op een paar? AntwoordBeste mr? p.s. de Winter,



home | vandaag | bijzonder | gastenboek | statistieken | wie is wie? | verhalen | colofon ©2001-2025 WisFaq - versie 3
| ||||||||||||||||||

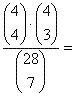
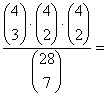

 Re: Kleurenpoker met 4 maal 7 kleurenkaarten
Re: Kleurenpoker met 4 maal 7 kleurenkaarten