WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Logaritmische vergelijking met verschillende grondgetallen

Hallo,

Ik moet de volgende vergelijking oplossen:

²log(3x) = ³log(2x)

het eerste wat ik heb gedaan is volgens de formule nlog(b) = log(b)/log(n)
Dus:

log(3x)/log(2) = log(2x)/log(3) Nu snap ik het niet meer. Kunt u mij er verder mee helpen?

Groetjes, S.
S
Leerling bovenbouw havo-vwo - donderdag 21 juni 2007

Antwoord

Beste S,

Gebruik nu log(ab) = log(a)+log(b) op log(3x) en log(2x) om de logaritmes in x in één lid te zetten en de rest in het andere lid. Dan krijg je:

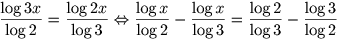
Nu kan je log(x) buiten haakjes brengen en delen door de coëfficiënt. Eventueel vereenvoudigen.

mvg,
Tom

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 21 juni 2007

Re: Logaritmische vergelijking met verschillende grondgetallen