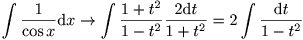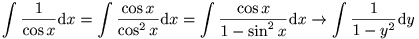|
|
|
\require{AMSmath}



Re: Re: Re: Primitieve van 1/cos(x)
Je zegt: een goed bruikbare substitutie is t=bgtan (x/2)
maar hoe werk je dan die integraal verder uit, want ik kom er niet!
M
Student Hoger Onderwijs BelgiŽ - zaterdag 2 juni 2007
Antwoord
Beste Mattis,
De voorgestelde substitutie was t = tan(x/2).
Dan is: cos(x) = (1-t2)/(1+t2) en dx = 2dt/(1+t2).
Hierdoor gaat de integraal over in:
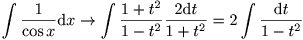
Nu kan je de noemer ontbinden in (1-t)(1+t) en splitsen in partiŽle breuken. Dan kan je direct integreren en terug t = tan(x/2) erin voegen.
Je kan die substitutie die nu een beetje "uit de lucht" komt gevallen, vermijden door dit trucje:
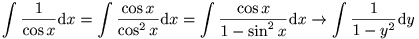
Waarbij in de laatste stap de voordehandliggende substitutie y = sin(x) werd toegepast. Dan opnieuw splitsen enz.
Je kan ook hier een kijkje nemen: Re: 2de moeilijke integraal berekenen.
mvg,
Tom

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 2 juni 2007
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 15041
Dit is een reactie op vraag 15041