WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oplossen sin2t

hoe los ik de volgende vergelijking op?

0.5sint+0.24sin2t=0.5sin1/4p+ 0.25sin1/2p?
0.5sin1/4p+ 0.25sin1/2p~0.6036
Ik heb sin2x al geprobeerd te vervangen zodat ik sinx op p kan stellen en zo gemakkelijk de vergelijking kan oplossen.
Ik kom er alleen niet uit!

Alvast bedankt!
Gea
gea
Leerling bovenbouw havo-vwo - zaterdag 12 mei 2007

Antwoord

let op!!

Het onderstaande antwoord klopt niet. Het maximum is t=pi/3. Er is dus een tweede oplossing net boven pi/3. Maar het juiste antwoord heb ik niet.

Ook met grof geweld kan ik geen oplossing vinden. Als je de vergelijking kwadrateert kun je alles in cost uitdrukken. Maar dan krijg je wel een vierdegraads vergelijking. Dat kun je ietsvereenvoudigen omdat je één oplossing (cost = 2^-0.5) al kent, maar dan houd je nog altijd een derdegraadsvergelijking over. Ook heb ik de voor de hand liggende "mooie" hoeken (5pi/12, 3pi/8) uitgeprobeert. Maar dat zijn geen oplossingen.
Ik vrees echt dat deze vergelijking geen mooie oplossingen heeft.

=======================

0.5sint+0.25sin2t=0.5sin1/4p+ 0.25sin1/2p

Ik heb 'm even geplot

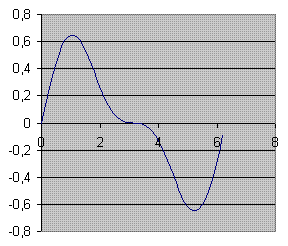
Je ziet dat het maximum erg dicht in de buurt ligt van de 0.6036 die jij hebt berekend. Als je de linker formule differentieert zie je dat het maximum inderdaad gelijk is aan t = p/4.

verder red je het wel denk ik? groet. oscar

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 12 mei 2007