WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

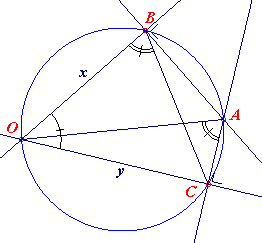
Bewijs

Twee rechten x en y snijden elkaar in een punt O en vormen een hoek a. Je kiest een willekeurig punt A, niet op de rechten gelegen en projecteert dit punt op x (punt B) en op y (punt C). Bewijs dat BC = OA sin a
bedankt!

Linda
Docent - zondag 7 januari 2007

Antwoord

Kijk eens naar de volgende figuur.

Daarin is OCAB een koordenvierhoek.
Nu is, volgens de sinusregel in driehoek OCB:
BC/sin(a) = OC/sin(OBC)
of
BC = OC/sin(OBC) · sin(a)
We moeten nu dus bewijzen dat OC/sin(OBC) = OA
En dat kan door gebruik te maken van de eigenschappen van de koordenvierhoek. Daarin is ÐOBC = ÐOAC.
Zodat in de rechthoekige driehoek OAC: OC/OA = sin(OAC) = sin(OBC). En dan is inderdaad OC/sin(OBC) = OA.
En het gestelde is dus juist!

En ook, zelfs zonder de sinusregel (Met dank aan FvL).
Is M (op OA) het middelpunt van de cirkel, dan is OA = 2r.
En ook: hoek BMC = 2a. Zodat (in driehoek BMC):
BC = 2r sin a = OA sin a.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 10 januari 2007