WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Kettingregel bij samengestelde functies

Hoe los je met behulp van een kettingregel een 'dubbele' functie op? Wat moet eerst?

Bijv:

^{(cos)²³√(cos5x⁴+8x)²}/_cos(8x)⁵

Hoe moet je dit aanpakken? =(
Jack
Leerling bovenbouw havo-vwo - woensdag 21 juni 2006

Antwoord

Beste Jack

Je opgave is een beetje verwarrend, wat doet die (cos) daar in het begin? Is het dan een 23e macht van die cosinus, van een 23e-machtswortel? In elk geval, je moet in het algemeen van 'buiten naar binnen' werken, wat er eerst komt moet je ook eerst afleiden. Ik zal het met een ander voorbeeld proberen te illustreren, dan kan jij het misschien toepassen op jouw voorbeeld.

Als je het één keer goed door hebt kan je het wellicht zonder gebruik te maken van tussenvariabelen. Voor de duidelijkheid zal ik die wel gebruiken, om het gebruik van de kettingregel te benadrukken. Ik neem een functie f(x) als volgt:

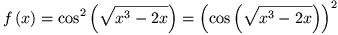
Die laatste gelijkheid heb ik er ter verduidelijking nog bij geplaatst, zo'n kwadraatje bij de cosinus betekent dat het de hele cosinus in het kwadraat is. Nu definieer ik de volgende hulpfunctie, steeds een stapje kleiner. Eerst zonder het kwadraat, dan het argument van de cosinus en dan nog de uitdrukking binnen die vierkantswortel:

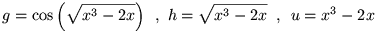
Volgens de kettingregel kan je nu de afgeleide van f naar x als volgt bepalen:

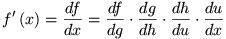
Maar door onze keuze van hulpfuncties hebben we nu dat:
f = g², g = cos(h), h = √u, u = x³-2x; zodat dit wordt:

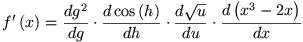
Deze afgeleiden zijn allemaal makkelijk te berekenen:

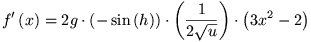
Dan vervangen we onze hulpfuncties terug naar de variabele x:

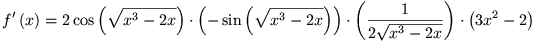
Uiteindelijk kan je nog wat vereenvoudigen:

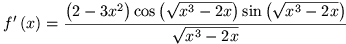
Zo zie je dat we een vrij ingewikkelde afgeleide via '4 schakels' gemakkelijk kunnen bepalen met de kettingregel.

mvg,
Tom

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 22 juni 2006

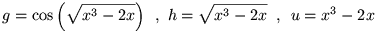
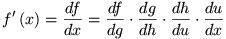
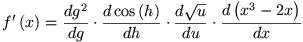
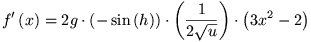
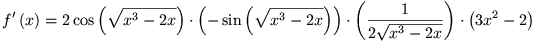
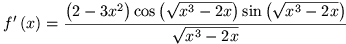
Re: Kettingregel bij samengestelde functies