|
|
|
\require{AMSmath}
Lengte van een kromme berekenen
Van een kromme met de volgende parametervoorstelling moet ik de lengte berekenen x=3cos2t y=cos3t
Welke integraal heb ik daarbij nodig en waarom? En hoe zit het met de lengte van de lus van de grafiek?
Mien
Leerling bovenbouw havo-vwo - dinsdag 11 april 2006
Antwoord
Ik neem aan dat je de kromme x=3cos(2t), y=cos(3t) bedoelt.
De periode van deze kromme is 2p.
Hieronder een plaatje van deze kromme
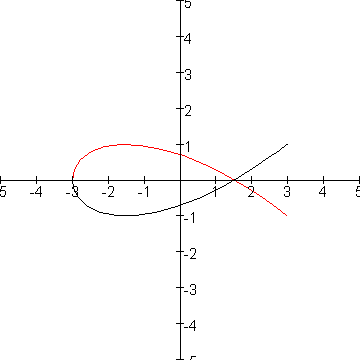
Op t=0 start de kromme in het keerpunt (3,1).
Uit y=0 volgt cos(3t)=0, dat betekent dus 3t=1/2p,11/2p,21/2p...
Dus de kromme snijdt de x-as voor t=1/6p, 1/2p,5/6p etc.
Het gedeelte van de kromme met t tussen 0 en 1/2p heb ik zwart getekent, het gedeelte van de kromme met t tussen 1/2p en p rood.
De lengte van de kromme is dus 2*0ò1/2pÖ((x '(t))2+(y '(t))2)dt.
Als je met de "lus" bedoelt het stuk van de kromme dat gelegen is tussen het punt waar hij zichzelf snijdt moet je als integratiegrenzen nemen de twee opvolgende t-waarden die bij dit punt horen.
Dat zijn t=1/6p en t=5/6p
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 12 april 2006
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
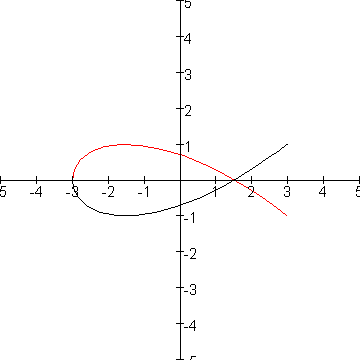
Re: Lengte van een kromme berekenen