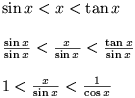WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Insluitstelling voor sin, cos en tan

Geachte heer/mevr,

Hoe zat het ook alweer:
Waarom is : Lim x®0 sinx / x = 1 ?
Lim x®0 tanx / x = 1 ?
Lim x®0 cosx / x = Bestaat niet?
Dank.
Maarte
Student universiteit - donderdag 9 maart 2006

Antwoord

Beste Maarten,

We beschouwen kleine waarden van x, vermits we de limiet naar 0 nemen. Tussen 0 en p/2 geldt sin(x) x tan(x). We vinden dan door insluiting:

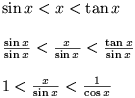
Vermits lim(x®0) 1/cos(x) = 1 hebben we de eerste limiet aangetoond.

De tweede kan je hieruit afleiden door tan(x) te vervangen door sin(x)/cos(x) en de factor 1/cos(x) naar voor te brengen, de vorige limiet blijft dan over.

De derde limiet geeft een 1 in de teller en 0 in de noemer, het teken hangt echter af van welke kant je naar 0 gaat zodat linker- en rechterlimiet verschillen, die laatste bestaat dus inderdaad niet.

mvg,
Tom

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 9 maart 2006