WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Limiet en afgeleide, bewijs regels

Ik heb 2 vragen over het bewijzen van regels.

Bewijs de regel f(x)=ax³ geeft f'(x)=3ax²
Ik kom uiteindelijk wel op het antwoord uit, maar ik weet niet of ik het heb goed gedaan en waarom het zo moet.
Dit heb ik gedaan:
f'(x)= lim (a(x+h)³-ax³)/h
h®0
haakjes vervolgens uitgewerkt
lim 3ax²+3axh+ah²
h®0

h0
3ax²(+0+0)=3ax²

De volgende snap ik helemaal niet:
Bewijs de regel f(x)=ax²+bx+c geeft f'(x)=2ax+b

Als voorbeeld in het boek staat ook
Bewijs de regel f(x)=ax² geeft f'(x)=2ax
f'(x)=lim (f(x+h)-f(x))/h
h®0

=lim (a(x+h)²-ax²)/h
h®0
Nou snap ik niet waarom en hoe deze stap gaat^^
Wat eigenlijk ook het probleem is van mijn eerste vraag.
Het zou fijn zijn als ik hier antwoord op zou kunnen krijgen.

Alvast bedankt,
Lisanne

Lisann
Leerling bovenbouw havo-vwo - vrijdag 20 januari 2006

Antwoord

Beste Lisanne,

Ik snap het probleem niet zo goed want volgens mij doe je het prima.
Misschien netjes uitgeschreven:

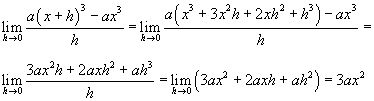
Voor f(x) = ax² gaat het ook zo, je werkt de haakjes uit, de term ax² valt weg, je kan een factor h wegdelen (dan is de noemer ook weg) dan nog h gelijk aan 0 nemen.

Voor f(x) = ax²+bx+c kan je de afgeleide van de drie aparte termen aantonen, afleiden is immers lineair.

mvg,
Tom

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 20 januari 2006

Re: Limiet en afgeleide, bewijs regels