WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Integralen

Beschouw de functie f(x) = (2x+4)e^-x
A(p) is de oppervlakte van het gebied ingesloten door de grafiek van f, de x-as en de rechte r - x=p met p$>$0

Ik dacht met partiële integratie en dan (2x+4) =u dus du=2 en e^-x is dan dv is dan e^-x
Dan kom ik: (-2p^-4/e^p) - 2/e^p + 6 uit. Maar volgens de oplossingen vanachter in het boek klopt dit niet. Maar ik zie echt niet de fout
Reactie
(2x+4) =u dus du=2 en e^-x is dan dv is dan e^-x en v is dan -e^x
dan kom ik uit:
(2x +4) (-e^-x) - (e^-x) .2
En door dan p en 0 in te vullen bekom ik dan die rare uitkomst met p.
(f(p) - f(0))

Marijk
3de graad ASO - zaterdag 19 november 2005

Antwoord

Je hebt dus als primitieve gevonden: F(x)=(2x+4)*-e^-x-2e^-x
Dit is gelijk aan F(x)=(-2x-6)e^-x.

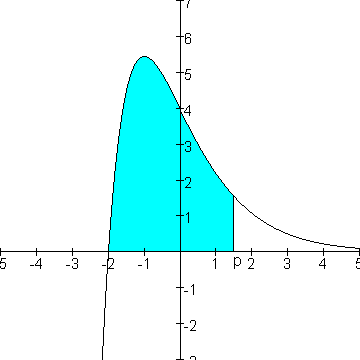
Als grenzen neem je nu: x=-2 en x=p, zodat je voor de oppervlakte krijgt:
F(p)-F(-2)=)=(-2p-6)e^-p-(4-6)e²=
=(-2p-6)e^-p+2e²

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 20 november 2005