|
|
|
\require{AMSmath}



Hoogte van een gelijkzijdige driehoek
Ik heb een oefening waar ik niks van begrijp:
"Bereken op hele centimeters nauwkeurig de hoogte van een gelijkzijdige driehoek waarvan een zijde 10 cm lang is."
Groetjes...
Ben
Iets anders - dinsdag 27 augustus 2002
Antwoord
Beste Ben,
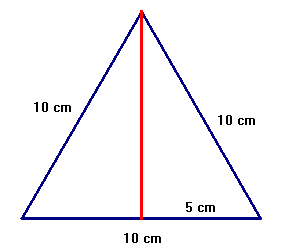
Zo ziet jouw driehoek eruit. Het is een gelijkzijdige driehoek (en dus zijn alle zijden gelijk, duswel evengroot: 10 cm) en je moet de hoogte berekenen die ik heb aangegeven met een lijn die de driehoek precies in tweeën deelt. Het enige wat je hoeft te doen, is de stelling van Pythagoras gebruiken  . .
Deze gebruiken we dan op één van de twee helften van de grote driehoek. Het maakt totaal niet uit welke, ze zijn precies hetzelfde.
Wat weten we? We gaan invullen wat we weten:
a2 + b2 = c2
a2 + 52 = 102
a2 + 25 = 100
De rest blijkt wel 
a2 = 100 - 25 = 75
a = √75  9 cm 9 cm
8,66 wordt afgerond op hele cm's zoals in de opdracht staat, dus dat wordt dan 9 cm.
De driehoek ik 9 cm hoog,
Ik hoop dat het duidelijk is 
bk
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 27 augustus 2002
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|









 .
. 9 cm
9 cm
 Re: Hoogte van een gelijkzijdige driehoek
Re: Hoogte van een gelijkzijdige driehoek