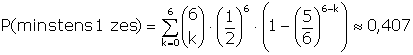|
|
|
\require{AMSmath}



Re: Re: Warhammer
Ah... volgens mij weet ik nu waar ik onduidelijk ben geweest.
Wat ik bedoelde is dit: je gooit 6 dobbelstenen.
Alle dobbelstenen waarmee je een 4, een 5 of een 6 hebt geworpen leg je apart (dat kunnen ze alle zes zijn, maar ook geen één).
Daarna probeer je met de (al dan niet) overgebleven dobbelstenen een 6 te gooien.
R.H.M.
Iets anders - zondag 23 oktober 2005
Antwoord
Dat verandert de zaak...
Noemen we X het aantal dobbelstenen met 4, 5 of 6 bij de eerste worp. Vervolgens bereken je P(X=0), P(X=1),... enz... deze kansen vermenigvuldig je dan met de kans om met 6, 5, 4,... dobbelstenen minstens één zes te gooien. In formulevorm krijg je dan:
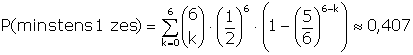
Of je zet alles in een Excelblad natuurlijk. Je krijg dan zoiets als:
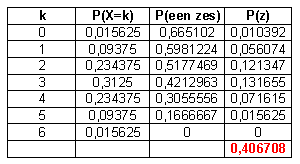
De gebruikt formules:
In de kolom P(X=k): =COMBINATIES(6;B4)*0,5^6
In de kolom P(een zes): =1-(5/6)^(6-B4)
In de kolom P(z): =C4*D4
En dan de kolom optellen.
Maar bedenk dat dit dus de kans is om in de tweede worp minstens 1 zes te gooien... en dat is ook weer iets anders dan de kans om in het totaalresultaat minstens 1 zes te gooien... dat kan je natuurlijk ook uit rekenen... maar dat is dan weer iets heel anders.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 23 oktober 2005
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 41025
Dit is een reactie op vraag 41025