|
|
|
\require{AMSmath}



Vergelijking met absolute waarden
Hoe los je deze vergelijking op?
|2x-6|+|x-5|=|1/2x-4|
Jullie gaven me de tip de grafieken te maken, maar hiermee is de vergelijking toch niet opgelost?
petron
Student hbo - woensdag 14 augustus 2002
Antwoord
Inderdaad, daarmee is de vergelijking niet opgelost. Op Grafieken tekenen kan je bijvoorbeeld het programma Winplot vinden. Hiermee kan je de grafiek tekenen van f(x)=|2x-6|+|x-5| en de grafiek van g(x)=|½x-4|.
Ik krijg dan het volgende plaatje:
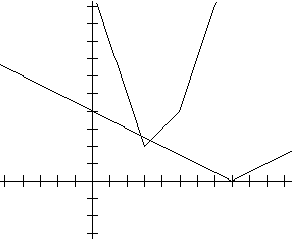
Met Twee-Snijpunten kan je het programma de snijpunten laten bepalen. Het programma geeft:
x=24/5
y=23/5
en
x=31/3
y=21/3
Dus de snijpunten zijn (24/5,23/5) en (31/3,21/3).
Is daarmee dan de vergelijking opgelost? In dit geval denk ik wel, maar is dit nu een 'goede' wiskundige manier om snijpunten te vinden?
Eigenlijk niet, want grafieken tekenen en de snijpunten aflezen is 'slechts' een benadering. Soms is dat meer dan genoeg, maar soms ook niet. Blijft de vraag hoe je dat dan moet doen...
En dat staat al beschreven bij Grafiek van een functie. Je maakt hierbij 4 verschillende gebieden:
|2x-6| verandert bij x=3, voor x<3 is dit hetzelfde als -2x+6 en voor x>3 is dit 2x-6
|x-5| verandert bij x=5, voor x<5 is dit -x+5 en voor x>5 is dit x-5
|½x-4| verandert bij x=8, voor x<8 is dit -½x+4 en voor x>8 is dit ½x-4
We krijgen nu eigenlijk 4 verschillende vergelijkingen met verschillende voorwaarden:
x 3 3 | 3 x x 5 5 | 5 x x 8 8 | x 8 8 | | -2x+6-x+5=-½x+4 | 2x-6-x+5=-½x+4 | 2x-6+x-5=-½x+4 | 2x-6+x-5=½x-4 | | -3x+11=-½x+4 | x-1=-½x+4 | 3x-11=-½x+4 | 3x-11=½x-4 | | 2½x=7 | 1½x=5 | 3½x=15 | 2½x=7 | x=24/5 | x=31/3 | x=42/7 | x=24/5 |
De antwoorden die NIET voldoen aan de voorwaarde heb ik doorgestreept
Zodat je uiteindelijk toch dezelfde antwoorden krijgt als hierboven, maar het is wel een hoop gedoe...

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 14 augustus 2002
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|









 3
3 x
x 8
8
