WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Grafiek tekenen van een functie

Hallo er zijn een paar dingen waar ik niet uitkom..

1) ik moet een de grafiek tekenen van de functie:

f:x - 1/(x-1) ... moet ik dan gewoon een x (bv x=3) invullen in de functie? dus voor x=3:
1/(3-1) = 0.5 ?

2) En dan moet ik ook de grafiek van de functie
f:x - |x² − 4| tekenen, moet ik dan ook gewoon een waarde van x in de functie invullen? dus bv voor x=3:
3² -4 = 5 enz.?

3) Hier kwam ik helemaal niet uit.. :
bepaal de afgeleide van de functies zonder rekenmachine:
a f(x)= (1+e^x)/(1-e^x)
b f(x)= ln(1+Öx)

4) En bepaal ò (e^x) / (e^x+1) dx ???

Ik snap 3 & 4 echt gewoon niet! kan ik het nog ergens terugvinden met een goede uitleg?

Heel erg bedankt!
Elif K
Student hbo - vrijdag 29 juli 2005

Antwoord

Hallo

Vooreerst zou ik je graag oproepen de spelregels van deze site eens te lezen. Vragen die alleen opgaven bevatten zonder meer worden hier niet beantwoord, zie regel 7 bij SPELREGELS. Lees ook regel 5 eens goed. Bijgevolg zal ik niet ingaan op je 3^e en 4^e vraag.

1) Ja, dat is de gebruikelijke manier van werken. Kies enkele punten, vb -1 0 1 2 3 4 en reken de functiewaarde (=y) uit. Je zal zien dat de functiewaarde in x=0 niet bestaat. Dit wijst op een verticale assymptoot.

2) Opnieuw kan je de waardes voor x invullen, maar dat is hier waarschijnlijk niet de bedoeling. De functie is een parabool in absolute waarde. Je moet eerst alle x'en zoeken waarvoor x²-4 positief is (tekenschema). Voor deze x'en is x²-4 = |x²-4|. Je tekent dus eerst gewoon de parabool x²-4 en voor de x'en waarvoor x²-4 positief is, lopen de grafieken van x²-4 en |x²-4| gelijk. Daarna bestuderen we de x'en waarvoor x²-4 negatief is (dit zijn alle andere). Voor deze waarden geldt: |x²-4| = - (x²-4) (denk daar maar eens over na). Teken nu dus de grafiek van -(x²-4). Voor alle x'en waarvoor x²-4 negatief is, loopt -(x²-4) samen met de grafiek van |x²-4|.

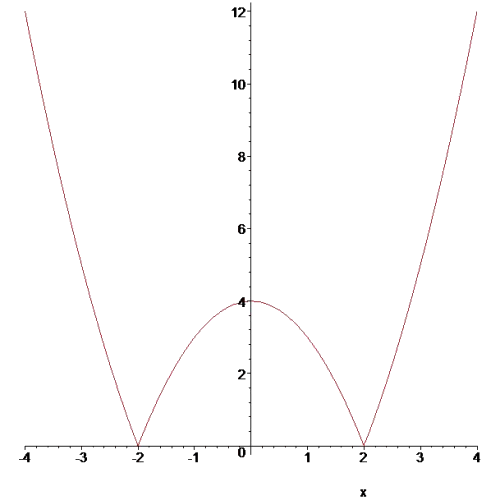
Opmerking: Je mag kiezen of je 0 als positief ziet, of als negatief
Opmerking: Voor de x'en waarvoor x²-4 negatief is, is de grafiek van |x²-4| dus gewoon de spiegeling rond de x-as van de grafiek van x²-4.

Groetjes

Igor

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 30 juli 2005