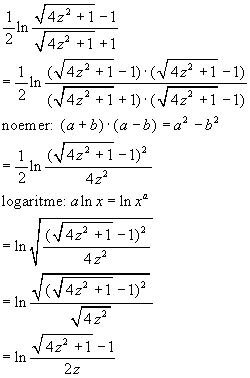WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Goniometrische substitutie omwentelingslichaam

Dit is een reactie op vraag 36423

(2)
Ik had het aanvankelijk ook geprobeerd met zo'n driehoekje maar wist niet wat ik met een halve hoek kon aanvangen. Bij deze bedankt voor de handige formule, die had ik blijkbaar over het hoofd gezien.

Helaas zou de juiste opl (1/2)ln [(Ö(4x²+1)-1)/(Ö(4x²+1)+1)] +c zijn ? Ergens een foutje binnengeslopen?

(3)
Bedankt! (N.B.:Tuurlijk was uw uitkomst correct!! )

Groetjes
Veerle
3de graad ASO - donderdag 7 april 2005

Antwoord

Beste Veerle,

Beide oplossingen zijn juist bij opgave 2. Afhankelijk van de methode of werkwijze die je hanteert bij het integreren kan je soms verschillende oplossingen vinden die correct zijn.

Ik zal even aantonen dat beide oplossingen geldig zijn:

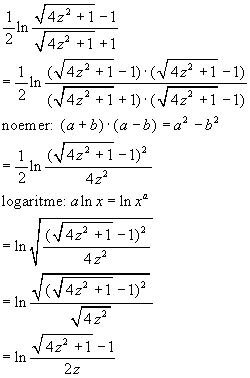
Je ziet dat er op het einde alleen nog een extra factor 2 in de noemer zit t.o.v. mijn oplossing, maar dat is geen probleem. Via eigenschappen van logaritmen kan je die wat ontbinden en zul je zien dat je die kan afzonderen als ln(1/2). Dit is een gewoon getal en kan dan vervat worden in de integratieconstante C.

Maar om zelf zeker te zijn, mag je natuurlijk altijd beide oplossingen afleiden en kijken of je de opgave terugkrijgt

mvg,
Tom

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 7 april 2005