WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Goniometrische substitutie omwentelingslichaam

Dit is een reactie op vraag 36364

(1)
Bedankt! Ik heb de oefeninge hermaakt en deze keer kwam het mooi uit!

(2)
Het spijt me maar deze begrijp ik nog steeds niet zo goed:

Na ò1/sint dt = ln|tan(t/2)| +c
Als dan t= Bgan(2z) , dan :
= ln|tan(Bgtan2z)/2| ??

(3)
Ik had in de titel geschreven '+omwentelingslichamen' zoals u wellicht hebt gemerkt valt er hier maar weinig te bespeuren m.b.t. dit onderwerp.
Bij deze :

Het punt p is het punt waar de grafiek van f(x)=x^3-3x een minimum vertoont. Door rotatie van het vlakdeel begrensd door de grafiek van f en de raaklijn in p rond deze raaklijn, ontstaat een ajuinvormig lichaam. Bereken de inhoud ervan.

Het punt p=(1,-2)
De raaklijn in p: y=-2
Wanneer ik het lichaam omwentelde rond de x-as (voor x=-2 en x=1) bekwam ik een negatieve waarde p*(-216/35) dus ik kwam er al gauw achter dat ik fout bezig was!

Hoe kan ik dus een figuur omwentelen rond een as dat noch de x- noch de y-as is?

Kan u me opnieuw een stukje verderhelpen?

Dank bij voorbaat...
Veerle
3de graad ASO - woensdag 6 april 2005

Antwoord

Beste Veerle,

2) Als je volgt dat òdt/sint = ln|tan(t/2)| (+C), dan moet je inderdaad nog terug substitueren.

Vermits 2z = tant = Bgtan(2z) = t heb je dan als oplossing: ln|tan(Bgtan(2z)/2)| (+C)

Dit zou je kunnen laten staan, ofwel pak je even een rechthoekige driehoek op een kladbladje en redeneer je aan de hand van SOS/CAS/TOA.
Bgtan(2z) wil zeggen dat je een hoek hebt waarvan de tan 2z is, bvb 2z op de overstaande zijde en 1 op de aanliggende zijde (dan is O/A inderdaad 2z).
De schuine zijde is Pythagoras, dus Ö(4z²+1).
De sinus is dan O/S: 2z/Ö(4z²+1)
De cosinus is dan A/S: 1/Ö(4z²+1)

Nu moet je even opletten, als we gewoon de Tan van die Bgtan namen, dan vielen die tegen elkaar weg. We zoeken echter de tangens van de halve hoek, en daar heb je deze formule voor:
tan(a/2) = (1 - cosa)/sina

Vul de gevonde waarden voor cos & sin in, en dan kan je nog wat vereenvoudigen.

Uiteindelijk vind ik als oplossing:
ln|(Ö(4z²+1) - 1)/(2x)| (+C)

3) P klopt en de vergelijking van de raaklijn ook!
Misschien even een figuur voor de duidelijkheid:

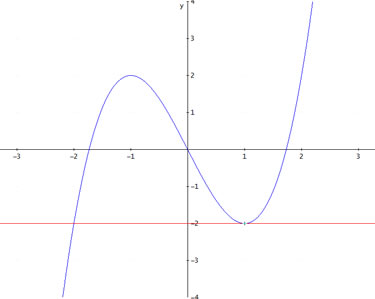
Als ik het goed begrijp is het dus dat linkerdeel dat we gaan wentelen om de raaklijn. Wat je zou kunnen doen is de functie omhoog verschuiven, zodat de raaklijn samenvalt met de x-as. Om de functie 2 plaatsen omhoog te verschuiven moet je 2 bij het beeld optellen, dit is dus de functie y = x³-3x+2

Deze heb ik even in het groen gezet:

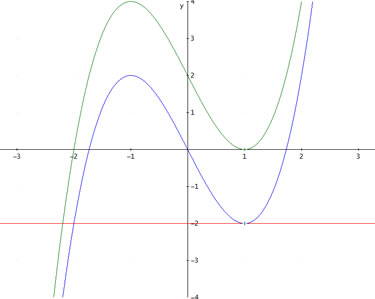
Zoals je kan zien is het identiek of je nu de blauwe grafiek wentelt om de raaklijn (y = -2) of de groene om de x-as (dit is immers de rechte met vgl y = 0, dus 2 hoger...)

De grenzen blijven verder gelijk, dus van -2 tot 1. Vermits het om een omwentelingslichaam gaat vermenigvuldig je de integraal met pi, en neem je als integrand f(x)².

Zelf kom ik 729p/35 uit, heb jij de juiste uitkomst?
Misschien begreep ik de vraag verkeerd of heb ik me misrekend, maar je snapt de bedoeling wel?

mvg,
Tom

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 6 april 2005

Re: Re: Goniometrische substitutie omwentelingslichaam