WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Het berekenen van de standaardafwijking

Opgave:
Bij een groep van 60 mensen werder IQ-tests afgenomen. Daarbij werd een volgend resultaat verkregen, opgedeeld in 11 klassen. :
IQ           Aantal(= Abs.Frq) Cum.Abs.Freq Cum.Rel.Freq.

[96,100[          3              3              5   
[100,104[         4              7             11,7
[104,108[         6              13              ...
[108,112[         6              19
[112,116[        12              31
[116,120[        10              41     
[120,124[         8              49
[124,128[         4              53
[128,132[         3              56
[132,136[         2              58
[136,140[         2              60
Ik berekende de cumulatieve absolute en relatieve frequentie.

Bereken de standaardafwijking en de variatiecoëfficiënt

We zagen de formule om de standaarafwijking te berekenen:
s²= (1/n)*å(x_i- x)² (x met een streepje boven, dus het rekenkundig gemiddelde = 116)

Ik weet echter niet welke waarde ik moet invullen voor x_i Ik dacht eerst aan 118 maar dat blijkt dan fout te zijn? Kan iemand me vertellen hoe ik de juiste standaardafwijking kan bekomen aub?

Hartelijk dank bij voorbaat,
Vele groetjes
hilde
3de graad ASO - zondag 13 maart 2005

Antwoord

Voor x_i vul je in: 98, 102, 106, 110, ...

Het handigst gaat dat met een tabel:

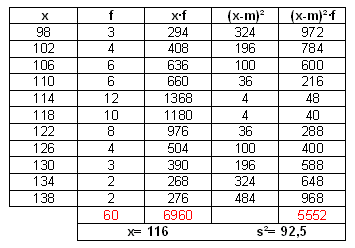
Kijk maar eens goed...

Zie eventueel ook 6. Standaarddeviatie

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 13 maart 2005