WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Driehoeksmeting

Dit is een reactie op vraag 3444

We zijn geloof ik een heel eind gekomen maar we lopen vlak voor het einde vast: Wat we tot nu toe hebben gedaan:
A levert op na ontbinding: x²+y²-2x-2y-34=0
B: x²+y²-16x-4y-52=0
C: x²+y²-2x-18y+57=0
A-B : 14x - 2y- 18=0
B-C :-14x +14y-109=0
--------------
12y-91=0
y=7.583
Als we y in de eerste vergelijking van A zetten dan:
x²-2x+57.4564-15.166-34=0
x²-2x=-8.2904
Wortelfunctie gebruiken
herleiden op nul : x²-2x+8.2904=0
a=1, b=-2 c=8.2904
x_1,2 = 2 +/- WORTEL 4-4·1·8.2904
--------------------------
2
dit levert een negatief getal onder de wortel. Oeps
Kunt U ons vertellen waar wij in de fout zijn gegaan in de berekening?

alvast bedankt voor jullie reactie
hans g
Leerling mbo - vrijdag 31 mei 2002

Antwoord

Ik zei al "als dat maar goed gaat". Als je een tekening maakt kan je zien wat er mis gaat:

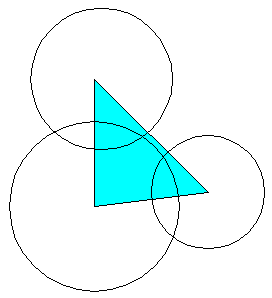
Wat is nu het snijpunt van deze drie cirkels?
Dat gaat dus niet... vandaar. Maar de methode op zich is wel goed...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 31 mei 2002