WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Goniometrie (sec en cosec)

Ik heb een oefening gekregen waar ik maar niet aan uit kan.
Kun je me A.U.B helpen??
hij gaat zo:
het punt P is het beeldpunt op de goniometrische cirkel van een georiënteerde hoek waarvan a een waarde is, dus P(cosa,sina). De loodlijn door P op de rechte OP snijdt de x-as en y-as respectievelijk in de punten U en V.
Bewijs dat co(U)= (seca,0) en co(V)=(0, cosec a)
Kun je me A.U.B op weghelpen
groetjes en dank bij voorbaat
anniek
3de graad ASO - zondag 13 februari 2005

Antwoord

Allereerst: ken je de definities van 'sec' en 'cosec'?
Iets als 'sec' is omgekeerde van de 'cos' en 'cosec' is omgekeerde van de 'sin'?
Of heb je de definities (in een rechthoekige driehoek) geleerd als:
- sec = schuine zijde gedeeld door aanliggende zijde;
- cosec = schuine zijde gedeeld door overstaande zijde?
Dan kijken we naar onderstaande figuur.

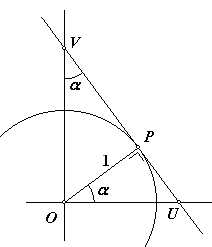
In driehoek OUP: cos(a) = 1 /OU, dus sec(a) = OU
En waarom is in driehoek OVP: Ð(OVP) = a?
In die driehoek: sin(a) = 1 / OV, dus cosec(a) = OV.

En doe dan maar iets met de functie co(van een punt).

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 13 februari 2005