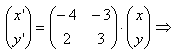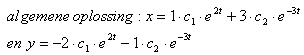WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Differentiaalvergelijkingen

hallo helper......!

ik kom maar niet uit deze vraag:

Bereken de algemene opl. van het volgende stelsel differentiaalvergelijkingen:

dx/dt= -4x -3y

dy/dt= 2x+3y

Bereken de bijz.opl. met beginwaarden x(0)=1 en y(0)=-2
Bereken de bijz.opl. met beginwaarden x(0)=3 en y(0)=-1

alvast bedankt,
groetjes
studen
Student hbo - vrijdag 14 januari 2005

Antwoord

Dit is een homogeen stelsel. De bijbehorende vergelijking is van de vorm z'(t)=A·z(t). Met A is een reele 2x2 matrix.

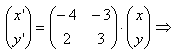
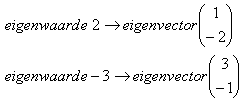
Nu is het even van belang hoeveel eigenwaarden deze matrix heeft. Gelukkig zijn dat er twee (dat is verreweg het makkelijkst).

Even de theorie bekijken dan zie je dat je daarbij de volgende oplossing krijgt:

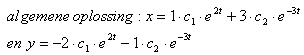
Nu nog even de beginwaarden invullen en vervolgens daaruit C₁ en C₂ berekenen.

Met vriendelijke groet
JaDeX

Zie Theorie stelsels differentiaalvergelijkingen

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 15 januari 2005