WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Stelling van Desargues

De stelling van Desargues wordt bewezen door de stelling van Menelaos toe te passen. Op t laatst vermenigvuldig je de deelverhoudingen en na enige ordening krijg je dan de omgekeerde stelling van Menelaos.
Maar waarom vallen de 2 andere producten weg?Zijn dat ook driehoeken met een transversaal?
Ik hoop dat jullie me kunnen helpen.....

TH
Leerling bovenbouw havo-vwo - donderdag 30 december 2004

Antwoord

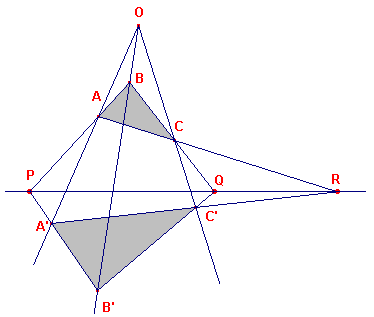
Bij bovenstaand plaatje vinden we (volgens de stelling van Menelaos):
(BCQ).(COC').(OBB') = 1
(CAR).(AOA').(OCC') = 1
(ABP).(BOB').(OAA') = 1
opvolgend met transversalen QC'B', RC'A' en PA'B' bij de driehoeken BCO, CAO en OAB.
Vermenigvuldiging van linker en rechter leden geeft (links) een product van 9 deelverhoudingen dat gelijk is aan 1.
In dat product staan bijvoorbeeld de factoren:
(COC') = C'C / C'O
en
(OCC') = C'O / C'C
Die twee deelverhoudingen met elkaar vermenigvuldigd geven (links) de waarde 1.
En dat doen (OBB') en (BOB') ook. En (AOA') en (OAA') ook.
Zodat we (links en rechts) overhouden:
(BCQ)(CAR)(ABP) = 1
En dus liggen Q, R, P op dezelfde lijn (omgekeerde stelling van Menelaos).

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 30 december 2004