WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Meetkundige betekenis inproduct

Kan iemand mij de meetkundige betekenis van het inproduct uitleggen?
kelly
2de graad ASO - donderdag 2 december 2004

Antwoord

Het inproduct van twee vectoren x, y geven we aan met (x , y). Noem de eindpunten van de vectoren A en B, beide met O als beginpunt.

In driehoek OAB is volgens de cosinusregel:
|AB|² = |OA|² + |OB|² - 2·|OA|·|OB|·cos($\angle$AOB)
Omgezet naar vectoren, aangegeven met de letters a en b:
|a-b|² = |a|² + |b|² - 2·|a|·|b|·cos($\angle$AOB)
Het linker lid uitgewerkt geeft:
|a-b|² = (a-b , a-b) = (a , a) + (b , b) - 2·(a , b)
of
|a-b|² = |a|² + |b|² - 2·(a , b)

Zodat:
(a , b) = |a|·|b|·cos($\angle$AOB)
Met andere woorden:

$\angle$AOB = arccos( (a , b) / (|a|·|b|) )

Iets meer(?) meetkundig kan het ook. Kijk daartoe naar de volgende figuur.

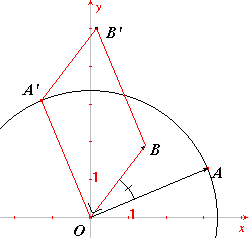
Ga zelf na, dat het inproduct iets te maken heeft met de oppervlakte van het parallellogram OBB'A.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 2 december 2004