WisFaq!

Meetkundige betekenis inproduct

Kan iemand mij de meetkundige betekenis van het inproduct uitleggen?

kelly
2-12-2004

Antwoord

Het inproduct van twee vectoren x, y geven we aan met (x , y). Noem de eindpunten van de vectoren A en B, beide met O als beginpunt.

In driehoek OAB is volgens de cosinusregel:
|AB|² = |OA|² + |OB|² - 2·|OA|·|OB|·cos($\angle$AOB)
Omgezet naar vectoren, aangegeven met de letters a en b:
|a-b|² = |a|² + |b|² - 2·|a|·|b|·cos($\angle$AOB)
Het linker lid uitgewerkt geeft:
|a-b|² = (a-b , a-b) = (a , a) + (b , b) - 2·(a , b)
of
|a-b|² = |a|² + |b|² - 2·(a , b)

Zodat:
(a , b) = |a|·|b|·cos($\angle$AOB)
Met andere woorden:

$\angle$AOB = arccos( (a , b) / (|a|·|b|) )

Iets meer(?) meetkundig kan het ook. Kijk daartoe naar de volgende figuur.


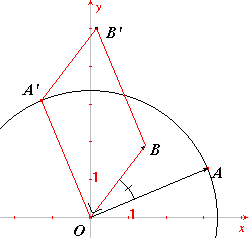
Ga zelf na, dat het inproduct iets te maken heeft met de oppervlakte van het parallellogram OBB'A.

dk
2-12-2004