WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oplossen

Hallo,
ik had even een vraagje...
Ik heb een functie gekregen waarbij ik f(x)=2 moet oplossen. De functie = f(x)=1+tan2x
Dan krijg je: 1+tan2x=2
tan2x=1
Maar hoe krijg je die 2 daar weg?

Kan iemand mij ook uitleggen hoe je aan de gemeenschappelijke periode van 2 functies komt?
Bijvoorbeeld: f(x)=cos0,5x en g(x)=sin(x-1/3x)
en van: sin pi x en g(x)=cos2/3 pi x

Alvast bedankt,
Milene

Milene
Leerling bovenbouw havo-vwo - woensdag 24 november 2004

Antwoord

Hallo,

die 2 hoef je niet noodzakelijk weg te krijgen. Je weet immers dat een tangensfunctie 1 wordt als haar argument (hier 2x) gelijk is aan p/4.
Dus tan(2x) wordt 1 als 2x=p/4 met andere woorden als x=p/8

Voor de gemeenschappelijke periode volstaat het het kleinste gemeen veelvoud te nemen van beide periodes.

Vb: sin(px) en cos(2px/3)
De periode van de eerste is 2, de periode van de tweede is 3. De gezamelijke periode is het kleinste gemeen veelvoud, nl 6.
Hier zie je een figuurtje:

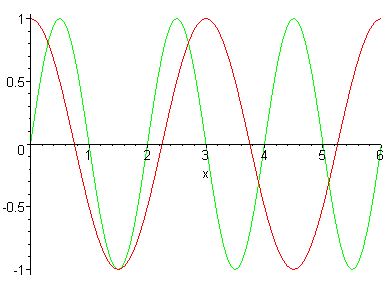
De groene is de sin(px) en de rode is de cos(2px/3)

Koen

PS: Mocht ja alsnog willen weten hoe je tan(2x) schrijft in functie van tan(x), klik dan op onderstaande link.

Zie Link

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 24 november 2004