WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Goniometrische vergelijkingen

hoi!
Ik ben bezig goniometrische vergelijkingen te oefenen. M.b.v. het tekenen van de grafieken komt het helemaal goed, maar op een andere manier niet. Zo snap ik dit voorbeeld niet eens:(:
sin(x)=0 $\to$ x=k+$\pi$ (Vanwaar die k? Wat wordt ermee bedoeld?)
sin(x) = ¹/₂
sin(x) = sin($\pi$/6)
sin(x) = sin($\pi$/6+kx₂$\pi$)
sin(x) = sin(5$\pi$/6+kx₂$\pi$)
$\to$ x = $\pi$/6 +kx₂$\pi$ $\angle$ x=(5$\pi$)/6 +kx$\pi$

alvast hartstikke bedankt!
loesje
Leerling bovenbouw havo-vwo - woensdag 10 november 2004

Antwoord

als je de vergelijking sin(x)=0 wilt oplossen, kan het helpen het grafiekje van sin(x) er even bij te pakken:

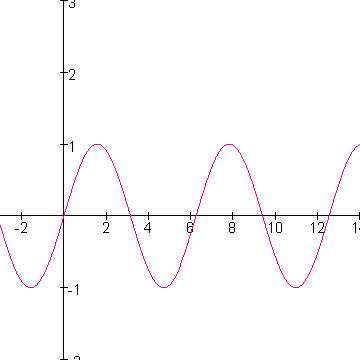
sin(x)=0 wil eigenlijk zeggen:
'voor welke waarden van x is sin(x) gelijk aan nul', ofwel voor welke waarden van x snijdt sin(x) de x-as?
Je ziet aan de grafiek dat op x=0 de grafiek de x-as snijdt, maar ook op x=$\pi$ (@3,14), maar ook op x=2$\pi$ (@6,26), maar ook op x=3$\pi$, etc....

het antwoord luidt samengevat: x=k.$\pi$ (en geen k+$\pi$ !)
Wij gebruiken trouwens als maal-teken een puntje.
Dan betekent die k dat k=1 mag zijn of k=2 of k=3, als het maar een geheel getal is.
Merk op dat k ook -1 of -2 of -3 mag zijn want aan de negatieve kant loopt de grafiek ook gewoon door.

Nou sin(x)=1/2
Dit betekent: voor welke waarden van x snijdt de grafiek van sin(x) de lijn y=1/2?
Om dit te begrijpen, moet je weer even een schetsje maken voor jezelf:

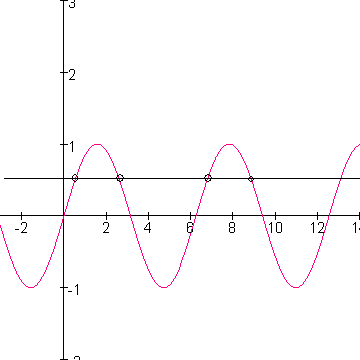
Je ziet aan het plaatje (plus eventuele tabel) dat voor x=1/6 $\pi$ de sinusgrafiek de lijn y=1/2 snijdt. (het eerste rondje van links, in de tekening) Echter de sinus heeft een periode van 2$\pi$ hetgeen betekent dat de grafiek zich iedere afstand 2$\pi$ volledig herhaalt.
Dus op x= 1/6$\pi$ + 2$\pi$ is er weer een snijpunt (het derde rondje van links),
en op x= 1/6$\pi$ + 4$\pi$ etc..

dus x= 1/6$\pi$ + k.2$\pi$ met k=1,2,3,....

Kijk goed naar de tekening, want evenver aan weerszijden van de top van de grafiek gaat de grafiek door y=1/2 heen.
dus niet alleen x=1/6$\pi$ maar ook x=$\pi$- 1/6$\pi$ is een geldige oplossing.
ofwel x=5/6 $\pi$.
aangezien de grafiek zich over afstand 2$\pi$ herhaalt, is
x= 5/6 $\pi$ + 2$\pi$ evengoed een oplossing.
en ook x= 5/6 $\pi$ + 4$\pi$, ..etc.

met andere woorden x= 5/6 $\pi$ + k.2$\pi$ (k=1,2,3,...) zijn eveneens oplossingen.

Dit alles samengevat, levert:
x=1/6 $\pi$ + 2.k.$\pi$ $\angle$ x= 5/6 $\pi$ + 2.k.$\pi$
met k=1,2,3,4,...

merk op dat het NIKS uitmaakt of je nou over k.2$\pi$ spreekt, of over 2.k.$\pi$. Het is lood om oud ijzer.

groeten,

martijn

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 10 november 2004