WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Tekenen in het complexe vlak

Hoi,
Hoe kan ik het volgende getal in het complexe vlak tekenen als Z is een element van C (de complexe getallen)
Z+2 en 1/Z

Alvast bedankt
Groetjes Linda
Linda
Student universiteit - vrijdag 5 november 2004

Antwoord

dag Linda,

Voor optellen en aftrekken van complexe getallen kun je gewoon de reële delen en imaginaire delen apart optellen of aftrekken.
Voor de tekening geldt dan de 'kop-staart-constructie'.

Applet werkt niet meer.
Download het bestand.

Complexe getallen vermenigvuldigen of delen kan handiger via de exponentiële vorm
z = r·e^i·$\Phi$
Neem twee complexe getallen
z₁ = r₁·e^i·$\Phi$1
z₂ = r₂·e^i·$\Phi$2
Dan is
^z₁/_z₂ = ^r₁/_r₂·e^{i·($\Phi$1-$\Phi$2)}

Neem nu z = r·e^i·$\Phi$
Nu moet je ¹/_z tekenen.
Dat is dus:
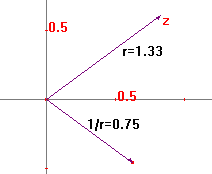
¹/_z = ¹/_r·e^{i·(0-$\Phi$)} = ¹/_r·e^i·(-$\Phi$)
Je moet voor de richting dus spiegelen in de reële as, en voor de lengte moet je 1 delen door de lengte van z

succes,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 5 november 2004