WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Scoreverloop en getallen

Vraag 1
Een team won een wedstrijd met 7-4.
Vraag: hoeveel verschillende mogelijkheden zijn er voor het scoreverloop als dit team niet achter heeft gestaan?

Vraag 2
Hoeveel (positieve gehele) getallen zijn er die kleiner zijn dan 56000 en waarvan de cijfers verschillend zijn?

Alvast bedankt!!
irene
Leerling bovenbouw havo-vwo - donderdag 21 oktober 2004

Antwoord

Vraag 1
Teken een roosterdiagram, maar zorg dat je alleen punten gebruikt waarbij team 1 voor (of gelijk) staat. Dat ziet er zo uit:

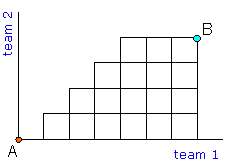
Zet de enen op goede plaatsen, optellen op de gebruikelijke manier en... het zou moeten kunnen.

Zie Roosterdiagrammen

Vraag 2
Voor het eerste cijfer kan je kiezen uit 1, 2, 3, 4 of 5. We bekijken eerst even 1 t/m 4.

I.
Als je 1, 2, 3 of 4 kiest voor het eerste cijfer, dan kan je voor het tweede cijfer kiezen uit 9 andere cijfers, voor het derde uit 8, het vierde uit 7 en het laatste cijfer uit 6. Dus er zijn:

4·9·8·7·6 mogelijkheden

II.
Als je 5 als eerste cijfer kiest dan kan je voor het tweede cijfer kiezen uit 1, 2, 3, 4. Het cijfer 5 heb je al gebruikt en 6 kan niet omdat het getal kleiner moet zijn dan 56000.

Als je kiest voor 1 t/m 4 dan kan je voor het derde cijfer kiezen uit 8 cijfers, het vierde uit 7 en het laatste cijfer uit 6. Dus zijn er:

1·4·8·7·6 mogelijkheden

Tel alle mogelijkheden van I en II bij elkaar op en je bent er uit. Dit kan je natuurlijk ook doen met behulp van een (verkort) boomdiagram. (Misschien doe ik dat nog wel een keer...)

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 21 oktober 2004