WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oppervlakte van de kleinste vlakke figuur

Hallo!

Ik zit met hetvolgende in mijn maag:

Ik moet de oppervlakte bepalen van de kleinste vlakke figuur die begrensd wordt door de parabool y^2=4x , de rechte 2x-4 en de x-as.

Dit weet ik al:
y^2=4x is een liggende parabool met de top in (0,0)
deze heeft een snijpunt met de lijn in (4,4)

Het figuur kan ik met wel voorstellen met -volgens mij dus- zijn de volgende coördinaten van belang:
(0,0)
(2,0), snijpunt van de rechte met de x-as
(4,4) snijpunt van de parabool met de rechte

De primitieve wordt:
Ö4x =2Öx = 2.x^0,5 --- 4/3 x^1,5

maaarrr dan.... dan loop ik vast. Moet ik nog de primitieve nemen van de rechte??? en welke grenswaarden moet ik invullen??

Superbedankt alvast!
Groetjes
K
Leerling bovenbouw havo-vwo - donderdag 26 augustus 2004

Antwoord

Hieronder een plaatje:

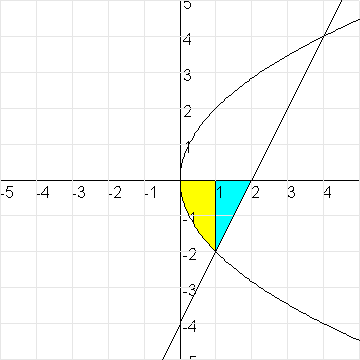
Het gaat dus om de oppervlakte van het gele en blauwe gebied samen.
De oppervlakte van het gele gebied is
-₀ò¹-2Ö(x)dx=₀ò¹2Ö(x)dx=[4/3xÖx]₀¹=1¹/₃
Het blauwe gebied is een driehoek. De rechthoekszijden van deze driehoek zijn 1 en 2, dus de oppervlakte van deze driehoek is ¹/₂*2*1=1.
De totale oppervlakte is dus 2¹/₃

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 26 augustus 2004