|
|
|
\require{AMSmath}



Methode van de hulphoek
Hallo
Ik begrijp eigenlijk de methode van de hulphoek f
totaal niet.
a sinx + b cos x = c
en je moet weten dat tan f gelijk is aan b/a
maar dan zit ik helemaal vast.
bv oefening.
3sinx + ÷3cosx = ÷6
Řsinx + ÷3/3cosx = ÷6/3
daarna zit ik vast.
en ik weet wel dat je dan die ÷3/3 kan schrijven als sin f/cosf omdat dit komt van tanf
maar dan?
alvast bedankt
vriendelijke groeten
randy
3de graad ASO - donderdag 8 juli 2004
Antwoord
Dag Randy,
Het heeft niet zoveel zin om door 3 te delen.
Je kunt beter delen door ÷(12) = 2÷3
Die 12 is het resultaat van 32 + ÷32
We beginnen dus met de vergelijking
a∑sin(x) + b∑cos(x) = c
De truc is het gevolg van een van de beruchte gonio-formules:
sin(x+f) = sin(x)∑cos(f) + cos(x)∑sin(f)
Het is nu de bedoeling om cos(f) de rol van de a te laten spelen, en sin(f) de rol van de b.
Dat kan niet zomaar, want je weet (hoop ik) direct dat er nooit een f gevonden kan worden zodat cos(f) gelijk is aan 3. Je weet immers dat voor elke hoek f geldt, dat
cos2(f) + sin2(f) = 1
Door nu slim de vergelijking te delen door ÷(a2+b2) hebben we dit voor elkaar:
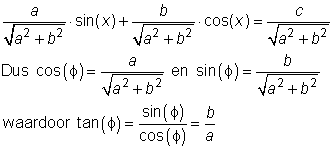
NB. Je moet nog wel even oppassen met het kwadrant van f: als a 0 dan ligt f in kwadrant 2 of 3, dus geldt: 0 dan ligt f in kwadrant 2 of 3, dus geldt:
f = arctan(b/a) + p
groet,

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 8 juli 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








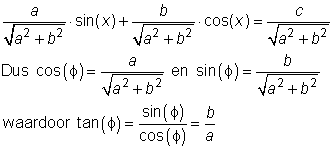
 0 dan ligt f in kwadrant 2 of 3, dus geldt:
0 dan ligt f in kwadrant 2 of 3, dus geldt:
