|
|
|
\require{AMSmath}
Maximale rechthoek met gegeven verhoudingen binnen gegeven rechthoek
Gegeven is een rechthoek van (bxh) 1500x1000
Hierbinnen wil ik een rechthoek plaatsen met gegeven verhoudingen (bxh) 3x1; zodat de hoekpunten van deze rechthoek op de rand van de buitenste rechthoek komen te liggen.
Hoe bepaal ik de hoek (en daarmee de bxh) van de rechthoek die ik erinleg
Waling
Iets anders - vrijdag 2 juli 2004
Antwoord
Dag Waling,
Ik doe maar gelijk het algemene geval: noem de breedte van de omhullende rechthoek a en de hoogte b.
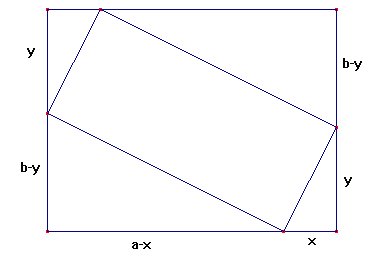
Je kunt dan twee vergelijkingen opstellen in x en y.
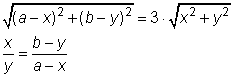
De eerste vergelijking volgt uit de gegeven verhouding.
De tweede vergelijking volgt uit de gelijkvormige driehoeken.
De eerste vergelijking kwadrateren geeft een kwadratische vergelijking die een cirkel voorstelt.
De tweede vergelijking kruislings vermenigvuldigen geeft ook een kwadratische vergelijking in x en y. Deze stelt een hyperbool voor.
In principe zijn er vier mogelijke oplossingen, waarvan sommige complex zullen zijn.
In dit specifieke geval zijn er in elk geval twee reële oplossingen, waarvan een met positieve waarden voor x en y:
x = 187.5 en y = 437.5
groet,
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 2 juli 2004
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
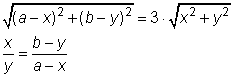
Re: Maximale rechthoek met gegeven verhoudingen binnen gegeven rechthoek