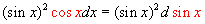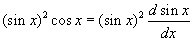WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Integreren van diverse functies

Dit is een reactie op vraag 25634

Hoi,
Ik begrijp het meeste wel van je uitleg, maar het meest essensiele begrijp ik niet; waarom mag je een bepaalde factor uit een functie halen, deze apart primiteren en dan achter de d zetten?

Sofie
Leerling bovenbouw havo-vwo - woensdag 23 juni 2004

Antwoord

Dat zal ik laten zien aan de hand van je eerste probleem:

òsin²x.cosxdx
Ik laat ten eerste dat integraalteken eventjes gemakshalve weg. Je wilt dus weten waarom:

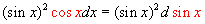
Waarom mag je hier de cosinus achter de d halen door te primitiveren?
Dit kun je het beste inzien door de dx in het linkerlid te verhuizen naar de noemer van het rechterlid:

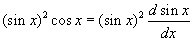
In het rechterlid zie je nu dat er staat:
dsinx/dx en dit is een andere schrijfwijze voor "de afgeleide van sinx naar x" of simpelweg [sinx]'.

Nu dezelfde redenering nògmaals, maar dan in algemene termen:
Stel je hebt twee functies. De ene noem je f(x) en de ander noem je g'(x).
dan geldt dat f(x).g'(x)dx gelijk is aan f(x)dg(x)
Waarom?
Omdat wanneer ik links&rechts deel door dx, dan staat er:
f(x).g'(x)=f(x).dg(x)/dx
en dit klopt als een bus aangezien dg(x)/dx betekent "de afgeleide van g(x) naar x" dus simpelweg g'(x).

Zodoende zie je dat je een factor achter de d mag halen door te primitiveren.

(de kunst zit em erin om zèlf te bepalen op welke manier je het handigst je f(x) en je g'(x) kiest)

groeten,
martijn

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 23 juni 2004