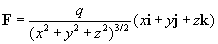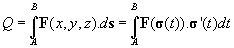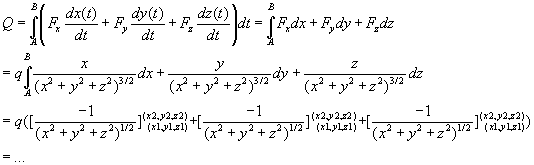|
|
|
\require{AMSmath}



Lijnintegralen
Lijntegraal:
Ik kwam dr niet uit, misschien kunnen jullie me helpen:
Let F= kr/r3 be the inverse-square force field of Example 16.2: F(x,y,z) = kr/r3 = (k(xi +yi + zk))/((x2+y2+z2)^(3/2))
Show that the work done by F in moving a particle from a distacne r1 from the origin to a point at distance r2 from the origin is given by: W=k((1/r1)-(1/r2))
Dank,
Martijn
Martij
Student universiteit - maandag 21 juni 2004
Antwoord
Die k die dient als constante noem ik maar even q, zodat we em niet door de war halen met de eenheidsvector k.
De kracht waarover we het hebben, is een omgekeerd-kwadratisch evenredig met de afstand. Dit zie je bijv. bij gravitatie- en bij electromagnetische krachten.
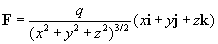
Verder geldt i.h.a. voor het uitrekenen van lijnintegralen dat
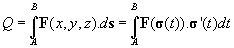
zie Integraal over curve in vectorveld
Alleen het probleem is hier, dat je a priori niet weet wat de precieze gedaante is van het pad s(t).
vandaar dat we stellen:
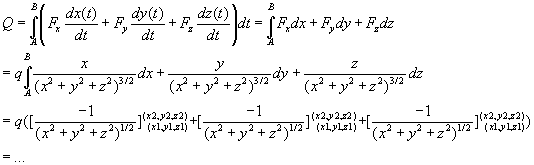
Vanaf daar kun jij de laatste stap waarschijnlijk wel zelf.
groeten,
martijn
mg
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 23 juni 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|