WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Hoe bereken je het zwaartepunt van een driehoek

Dit is een reactie op vraag 24126

Ik wil weten hoever het zwaartepunt verwijderd is van elke
hoek, bij gegeven zijdelengtes vd driehoek.
R.Trie
Iets anders - vrijdag 28 mei 2004

Antwoord

OK, leuke vraag wel.
De volgende eigenschap van de zwaartelijnen is hierbij van belang:
de zwaartelijnen van een driehoek verdelen elkaar in stukken die zich verhouden als 2:1, waarbij het grootste stuk de afstand tot het hoekpunt is.

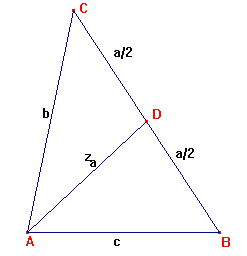
Nu kun je de lengte van de zwaartelijn uit hoek A, noem die z_a, uitdrukken in de zijden a, b en c met behulp van twee keer de cosinusregel: een keer in driehoek ABC en een keer in driehoek ADC.
Het resultaat is:
z_a = √(¹/₂b² + ¹/₂c² - ¹/₄a²)
Tweederde deel hiervan is dus de afstand van het zwaartepunt tot A.
Dergelijke formules kun je opstellen voor de afstanden tot B en tot C.
groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 28 mei 2004