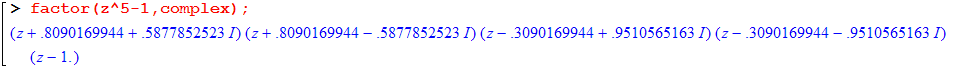WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Algebraïsch ontbinden

z⁵-1=0 hoe moet je dit algebraïsch ontbinden via complexe getallen?
brigan
3de graad ASO - zaterdag 8 mei 2004

Antwoord

Hoi,

Eerst gaan we z⁵=1 eens oplossen.
Ik hoop dat je de formule van Euler kent, z = re^iF, die stelt hetzelfde voor als z = a + bi, of z = r(cos(F) + isin(F)). Aangezien je weet dat alle drie de formules dezelfde voorstelling van een complex getal zijn, geldt dat er bij het argument 2kp mag opgeteld worden (de periode van cosinus en sinus, cos(F + 2kp) = cos(F) en dit geldt ook voor de sinus). Dit hebben we dadelijk nodig.

Dus z = re^iF Û z⁵ = (re^iF)⁵ Û z = r⁵e^5i(F+2mp). (Volgens de stelling van de Moivre).
En 1 heeft als modulus 1 en als argument 0 (+ 2kp), dus e^{i(0 + 2kp)} = e^i(2kp).
Aangezien z⁵ = 1 Þ r⁵e^5i(F+2mp) = e^{i(0 + 2kp)}.
Wanneer zijn twee complexe getallen hetzelfde? Als ze het reële evenals het complexe deel hetzelfde hebben, dus in ons geval r⁵ = 1 en 5i(F + 2mp) = i(2kp).
r = 1 en F + 2mp = ²/₅kp
r = 1 en F = ²/₅kp aangezien er altijd een veelvoud van 2p bij het argument mag opgeteld of afgetrokken (in ons geval -2mp) worden.

Een n-de graads vergelijking heeft precies n oplossingen (wortels), dus laten we k de waarden 0,1,2,3 en 4 aannemen.
Voor het gemak herschrijven we de gevonden r en F in de vorm z = r(cosF + isinF).

z₀ = cos(0) + isin(0) Þ z₀ = 1
z₁ = cos(²/₅p) + isin(²/₅p)
z₂ = cos(⁴/₅p) + isin(⁴/₅p)
z₃ = cos(⁶/₅p) + isin(⁶/₅p)
z₄ = cos(⁸/₅p) + isin(⁸/₅p)

De ontbinding is dus (z-1)·(z-cos(²/₅p)-isin(²/₅p))·(z-cos(⁴/₅p)-isin(⁴/₅p))·(z-cos(⁶/₅p)-isin(⁶/₅p))·(z-cos(⁸/₅p)-isin(⁸/₅p)).

Maple geeft de volgende benadering:

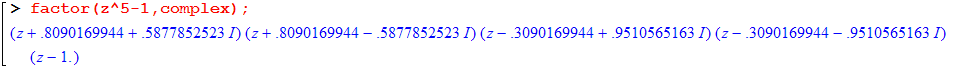
Groetjes,

Davy.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 9 mei 2004