WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Coördinaten van snijpunt berekenen van twee lijnen dmv vectorvoorstellingen

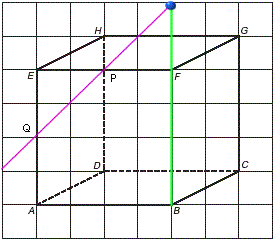
gegeven is een kubus ABCD.EFGH met ribbe = 6.
A = (0,0).
P is het midden ribbe EF.
Q is het midden ribbe AE.
Bereken de coördinaten van het snijpunt T van de lijn PQ
met de lijn BF. Dit moet berekend worden met vectorvoorstellingen, ik snap
er echt nix van?

André
Leerling bovenbouw havo-vwo - woensdag 14 april 2004

Antwoord

Je moet eerst de coordinaten van de hoekpunten berekenen.
Daarbij is uiteraard A niet (0,0) maar (6,0,0), B(6,6,0), C(0,6,0) en D(0,0,0), de punten E,F,G,H liggen precies boven respectievelijk A,B,C,D dus E(6,0,6), F(6,6,6), G(0,6,6) en H(0,0,6).
Nu geldt dat P het midden is van EF dus P(6,3,6) en Q is het midden van AE dus Q(6,0,3) maak nu een vectorvoorstelling van de lijn l door P en Q. De richtingsvector daarvan is p-q=(0,3,3) maar dan is (0,1,1) ook een richtingsvector.
De lijn PQ wordt nu (6,3,6)+l(0,1,1)
Nu zelf hetzelfde doen met BF en dan het snijpunt van deze lijnen berekenen.

Succes

JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 14 april 2004

Re: Coördinaten van snijpunt berekenen van twee lijnen dmv vectorvoorstellingen