|
|
|
\require{AMSmath}



Nederlanders op vakantie
Van de Nederlandse bevolking gaat 22% uitsluitend in Nederland op vakantie, 36% gaat uitsluitend naar het buitenland en 14% gaat zowel in Nederland als in het buitenland op vakantie. De rest gaat niet op vakantie.
Bij een onderzoek worden 80 Nederlanders ondervraagd.- Bereken de kans dat van tien willekeurig gekozen Nederlanders er twee uitsluitend naar Nederland op vakantie gaan, vier uitsluitend naar het buitenland gaan en de rest niet op vakantie gaat.
Ik heb al geprobeerd met 'binompdf' per gebeurtenis de kansen te berekenen, maar dat kan hier natuurlijk niet, omdat het 1 experiment is. Maar ik zou echt niet weten hoe ik deze kans kan beantwoorden.
Alvast bedankt,
Groetjes Dian.
dian
Leerling bovenbouw havo-vwo - vrijdag 2 april 2004
Antwoord
Dit is een voorbeeld van een kansprobleem waarbij de volgorde niet van belang is en de kans niet verandert ('met terugleggen'). Je zou (inderdaad) denken: 'binomiaal verdeling!'. Maar dat klopt niet, want het is geen 'ja/nee' probleem. In zo'n geval kan je de kans 'gewoon uitschrijven'.
We kiezen de volgende letters:
N: Nederland (p=0,22)
B: buitenland (p=0,36)
G: niet op vakantie (p=0,28)
De aanpak is dan:
1. Kies een goed rijtje
2. Bereken de kans op dat rijtje in die volgorde
3. Bereken hoeveel volgordes je kan maken
4. Bereken de kans
1.
Dit is een goed rijtje: NNBBBBGGGG
2.
P(NNBBBBGGGG)=0,222·0,364·0,284
3.
Hoeveel rijtjes kan je maken met NNBBBBGGGG?
Dat kan op 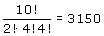 manieren. manieren.
Zie 6. Het bakjesmodel in voorbeelden
4.
De kans is...
Nu jij weer. Hopelijk helpt dat...
Zie ook Toepassingen van de piramide van Pascal

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 2 april 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








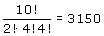 manieren.
manieren.
